で平均から大きく離れたところの生起確率の簡単な評価を与えました。今回はその評価をさらに精密にして、数理的な構造をもっと詳しく見たいと思います。前の記事で次の評価を与えました。
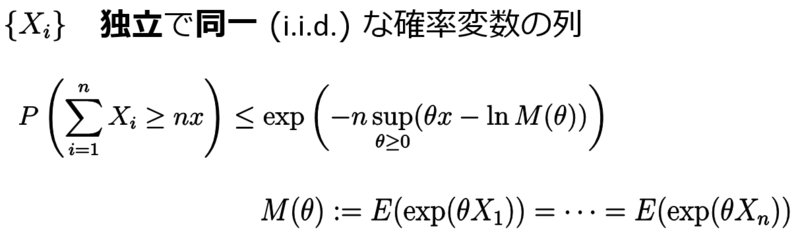
上の は確率変数
の積率母関数、
は確率変数
のキュムラント母関数 (物理では自由エネルギー) と呼ばれています。上の指数関数の中の
は
のもとで
の上限を意味しています。これを改造することで
の上界だけでなく下界も与えることができます。それがクラメールの定理です。
●レート関数
まず、上の評価式の中にある の
という制約を外した
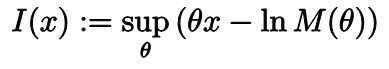
を考えましょう。この はキュムラント母関数をルジャンドル変換したものであり、レート関数と呼ばれています。レート関数は
で説明している理由で凸関数となっていることが分かります。また、レート関数は平均値で最小値0となることが以下のように分かります。

●大偏差原理
次の定理はクラメールの定理と呼ばれる大偏差原理です。

上の の存在の仮定は
が
で微分可能であることを保証するためにあります。この定理によって、平均から大きく離れたところの生起確率がレート関数
によって特徴付けられることが分かりました。証明に興味のある方は詳しくは参考文献を読んでいただくことにしますが、ポイントは次の通りです。

要するに以前説明した中心極限定理
を平均から大きく離れたところで適用できるように確率分布関数を改造するのです(平均から大きく離れたところの生起確率は単純に中心極限定理を適用しても見積れない。詳しくはこちら)。これは確率測度を変換していることを意味します。確率分布関数と確率測度の関係についてはこちらをご覧ください。
●レート関数とカルバックライブラー情報量
レート関数は前の記事で説明したカルバックライブラー情報量と次のように結びつきます。

もっと一般的な状況でレート関数とカルバックライブラー情報量の関係がありますが、興味のある方は参考文献を参照してください。
●参考文献
記事を書くときに参考にした文献です。
(1)大偏差原理の証明を参考にしました。

- 作者: Adam Shwartz,Alan Weiss
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 1995/09/01
- メディア: ハードカバー
- この商品を含むブログを見る
(2)凸関数やルジャンドル変換について詳しい説明が書いてます。

- 作者: Stephen Boyd,Lieven Vandenberghe
- 出版社/メーカー: Cambridge University Press
- 発売日: 2004/03/08
- メディア: ハードカバー
- 購入: 1人 クリック: 11回
- この商品を含むブログ (1件) を見る
(3) 大偏差原理のもっと深いことが書いてます。

Large Deviations Techniques and Applications (Stochastic Modelling and Applied Probability)
- 作者: Amir Dembo
- 出版社/メーカー: Springer
- 発売日: 2013/04/11
- メディア: Kindle版
- この商品を含むブログを見る
●予告
今回名前だけ出して説明しなかった凸関数やルジャンドル変換は情報を幾何学的に研究する学問の中でも重要な役割を果たします。次回からはしばらく情報幾何学について説明していきたいと思います。










































































































