超関数とは関数の概念を一般化したもので、もともとは物理の方で導入されたディラックのデルタ関数という計算に便利なものを数学的に正当化しようとして考え出されました。ディラックのデルタ関数は直感的にはガウス分布の確率密度関数の分散を0に限りなく近付けたときの極限関数が持つ性質を理想化したものです。
●ガウス分布とディラックのデルタ関数
まず、色々な分散のガウス分布の確率密度関数は次のようになっています。

ディラックのデルタ関数は次のようにガウス分布の確率密度関数の分散を0へ限りなく近付けたときの特徴を理想化したものと考えられます。

●ディラックのデルタ関数の変なところ
ディラックのデルタ関数 は次のように突っ込みどころ満載です。

このように 関数には変な部分があります。しかし、応用上は便利なので
関数を捨て去るのは勿体ないと変な部分を解消しようと努力した人がたくさんいました。その中でシュワルツという数学者は通常の関数の概念を一般化した超関数というものを創造することに成功しました。
●関数概念の一般化
シュワルツは次のように緩増加超関数というものを導入しました。ここで、 は
ogyahogya.hatenablog.comの中で定義したシュワルツ空間のことです。

緩増加超関数全体の集合は定義から の双対空間になっています。


緩増加超関数は通常の関数の一般化と考えることができます。そのことを見るために次のリースの表現定理というものを思い出しましょう。

このリースの表現定理を用いると、前の記事で議論した関数空間 は
に含まれるということが次のように分かります。

また, に含まれないディラックのデルタ関数も
に含まれます。ただし、ここでのディラックのデルタ関数は上で与えたような数学的に意味のないものではありません。
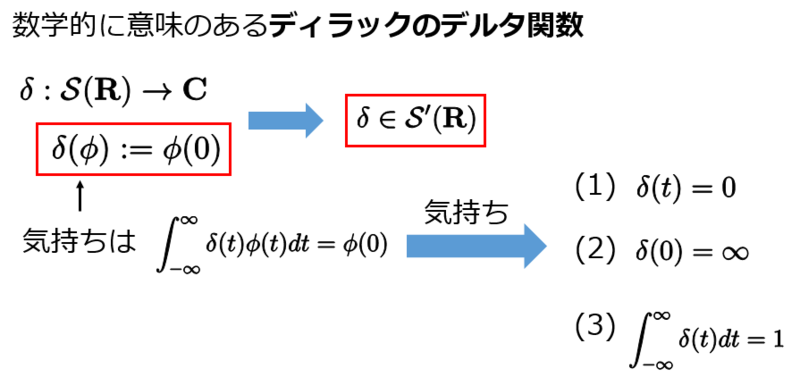
●超関数の積分による表示
通常の関数が与えられたら、その関数から積分を利用して緩増加超関数を次のように定義することができます。

これと同じように、今度は緩増加超関数を積分の形で書いてみましょう。例えばディラックのデルタ関数であれば次のようになります。

一般の緩増加超関数に対しては積分の形で書いていても積分の意味は持たないことに注意しましょう。しかし、気持ちを表現するのに便利なのでよく使われます。
次の例も緩増加超関数です。これはディラックのデルタ関数のちょっとした一般化になっています。

●超関数の微分
通常の関数として考えたときに微分できない関数も緩増加超関数として考えると微分できるようになります。まず緩増加超関数の微分を定義します。

緩増加超関数として微分ができるようになる関数の例としては次のものがあります。

また、ディラックのデルタ関数の微分は次のように認識できるようになります。

●ディラックのデルタ関数は合成積の単位元
実数の世界の中で任意の実数に1をかけても値を変えることはありません。この場合の1のように要素を変化させないものを単位元といいます。ディラックのデルタ関数は関数の合成積の演算を考えたときの単位元になっています。このことを示しましょう。合成積については
ogyahogya.hatenablog.comを参考にしてください。まず、通常の関数と急減少関数の合成積を緩増加超関数だと思って急減少関数に作用させると次のようになることに注意しましょう。

このことを参考に緩増加超関数と急減少関数の合成積を次のように定義します。
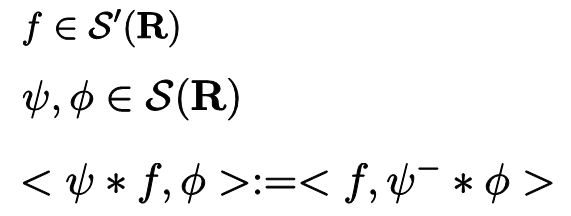
すると、ディラックのデルタ関数が合成積の中で単位元になっていることが次のように分かります。

また、二つの緩増加超関数の合成積は次のように定義します。

すると、次のような計算が可能になります。
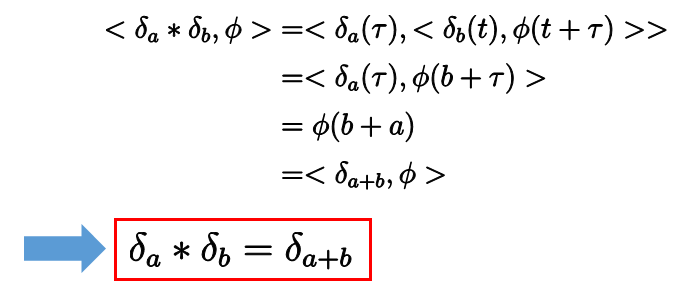
●超関数のフーリエ変換
前の記事で関数のフーリエ変換について説明しました。フーリエ変換は緩増加超関数に対しても次のように定義できます。
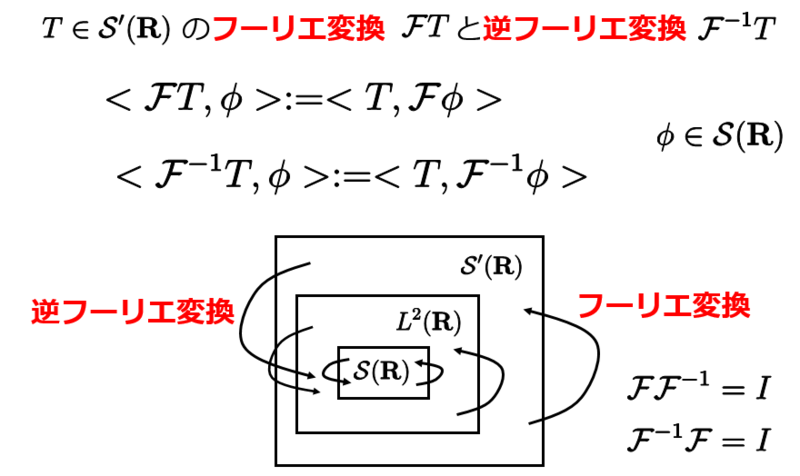
ディラックのデルタ関数のフーリエ変換は1になります。

このことは次のような解釈が可能です。

また、1のフーリエ変換はここではデルタ関数に を掛けたものになりますが、フーリエ変換の定義の仕方によっては単にデルタ関数になることもあります。

●合成積のフーリエ変換
前の記事で時間領域の合成積をフーリエ変換すると周波数領域での普通の積になるという話をしました。このことは緩増加超関数に対しても成り立ちます。

●参考文献
記事を書くときに参考にした文献です。
(1) スタンフォード大学の B. Osgood先生の講義資料の p152~p194まで。とても分かりやすい。
(2) 超関数のところを参考にした。分かりやすい。
(3) この記事で紹介した超関数を考えた人の本の和訳。この記事よりも高度なことが書いてある。

- 作者: L.シュワルツ,Laurent Schwartz,岩村聯,石垣春夫,鈴木文夫
- 出版社/メーカー: 岩波書店
- 発売日: 1971/09/30
- メディア: 単行本
- クリック: 5回
- この商品を含むブログを見る
●予告
確率論では確率測度としてディラック測度というものを考えることがよくあります。これがここで紹介したディラックのデルタ関数とどんな関係があるかということや、いくつかの確率測度の紹介をしたいと思います。その次に、中心極限定理の話へ進みたいと思います。
