対象とする線形システム
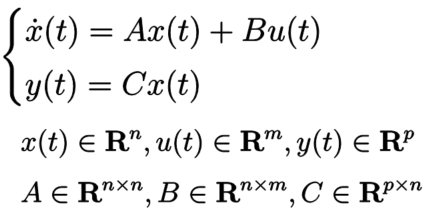
の可制御性と可観測性の定義は
で紹介しましたが、この記事では可制御性と可観測性の「大きさ」を定量的に測る手段を紹介します。線形システムについては
で紹介しています。この記事の中では行列 を安定、つまり、
のすべての固有値の実部は負であると仮定します。
入力エネルギー最小化問題
まず、線形写像 を
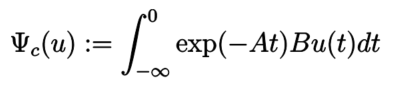
と定義します。ここで、 は区間
上で定義された2乗可積分な関数全体の線形空間です。このような空間については、
でも紹介しています。この は無限の過去
に状態が0であるときの現在
の状態
を表していると解釈できます。実際に、
とすると、行列
が安定なので、\begin{align}
x(0) &= \lim_{t_0\rightarrow -\infty}\left(e^{-At_0}x(t_0)\right) + \int_{-\infty}^0 e^{A(0-t)}Bu(t)dt\\&=\int_{-\infty}^0 e^{-At}Bu(t)dt = \Psi_c(u)
\end{align}となるからです。
とするとき、
によって
を定義し、
によって
を定義します。
このとき、次の入力エネルギー最小化問題を考えます。
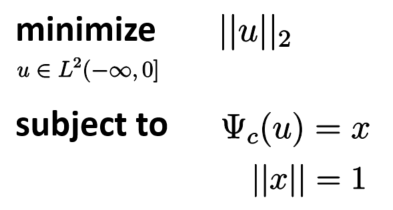
ただし、 はユークリッドノルムを表します。この問題は、「状態を原点から単位球面上に到達させることが可能な2乗可積分な入力の中で、エネルギーが最小になるものを求めよ。」ということを意味しています。
可制御性グラミアン
上の入力エネルギー最小化問題と次の可制御性グラミアン

は密接な関係があります。ここでは、その関係を見るための準備をします。
線形作用素 と行列
の間には次の関係が成り立ちます。
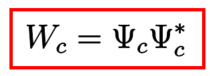
ここで、 は
の共役作用素です。共役作用素はこちらで説明しましたので、興味がありましたら参照してください。
上の関係が成り立つことは次のように確認できます。
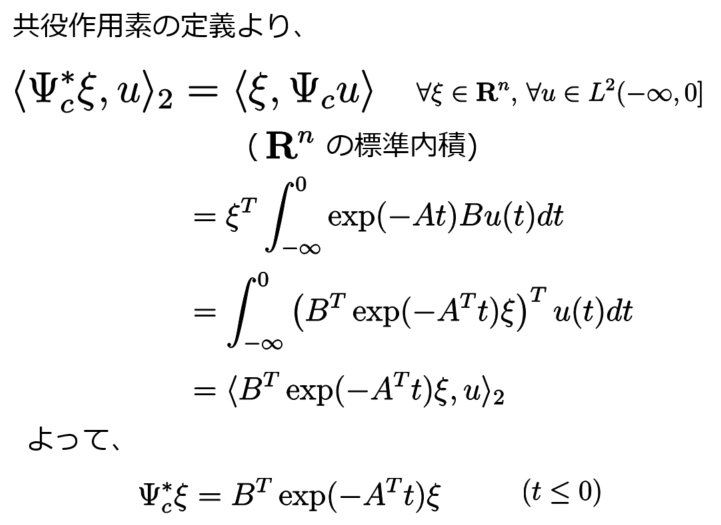

任意の に対して、上記の式が成り立つことから
が成り立つことが証明できました。
可制御性グラミアンの表式から は半正定値対称行列だということが分かります。実は、線形システムが可制御であることと、
が正定値対称行列であることは等価です。ここでは簡単のために、線形システムは可制御であるとして話を進めます。
直交射影
入力エネルギー最小化問題の解と可制御性グラミアンの関係を、すっきりと理解するために、直交射影の概念を紹介します。
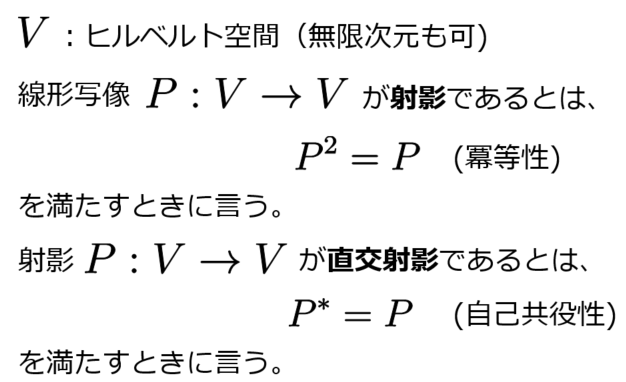
直交射影には、次の性質があります。

入力エネルギー最小化問題の解と可制御性グラミアンの関係
入力エネルギー最小化問題の解は、次のように可制御性グラミアン を用いて表現できることが分かります。

実は、ある直交射影 が存在し、(※)を満たす任意の
に対して、
となって
も(※)を満たすことが示せます。直交射影の定義の下で示したように、
なので、上の主張が成り立つということになります。
そのような直交射影 は
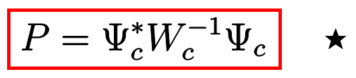
で与えられます。 が(※)を満たすことは、
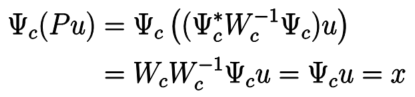
から分かります。さらに、★が直交射影であることも少し計算すれば示せます。
さらに、入力エネルギーと可制御性グラミアンの間には、次の関係が成り立つことが分かります。
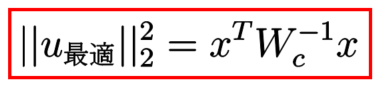
なお、 の逆行列
は、線形システムを可制御であると考えているので存在します。
可制御性グラミアンの幾何学的解釈
ここでは、入力 (
) で到達可能な状態を可制御性グラミアン
を用いて特徴付けます。この特徴付けは次の事実に基づきます。
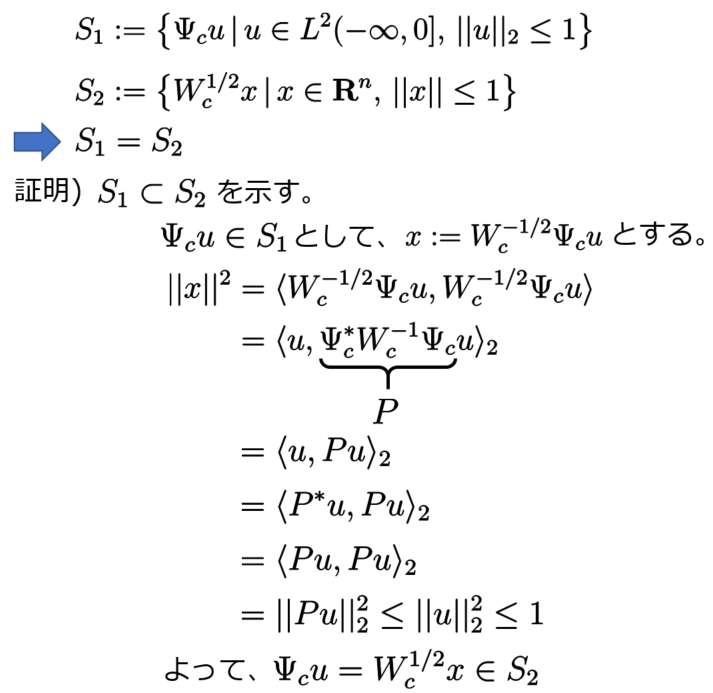

上で示したことから、入力 (
) で到達可能な状態は
(
)だということが分かりました。
以上のことから「可制御性の大きさ」、すなわち、「制御のしやすさ」と可制御性グラミアン の関係を調べることができます。このことを見るために、単位エネルギー
の入力
で到達可能な状態の集合は

であることに注意しましょう。今、 の固有値を
、対応する正規直交固有ベクトルを
とすると、

となり、 は固有ベクトル
の方向を主軸として固有値
を主値とする楕円であることが分かります。イメージ図は下のような感じです。
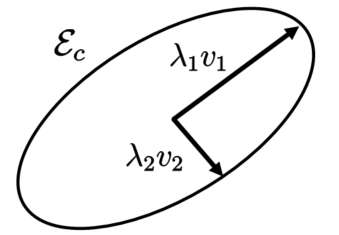
つまり、単位エネルギー の入力
で原点から最も遠くまで到達可能な方向が可制御性グラミアン
の最大固有値に対応する固有ベクトルの方向で、2番目に遠くまで到達可能な方向が2番目に大きい固有値に対応する固有ベクトルの方向、3番目に・・・ということになります。言い換えると、最も制御しやすい方向が可制御性グラミアン
の最大固有値に対応する固有ベクトルの方向で、最も制御しにくい方向が
の最小固有値に対応する固有ベクトルの方向だということです。
以上から、線系システムが可制御であっても、制御のしやすい方向としにくい方向があり、それらを定量的に調べるためには可制御性グラミアン の固有値と固有ベクトルを調べれば良いということが分かりました。
可観測性グラミアン
次に、観測のしやすさを定量的に評価する可観測性グラミアンについて説明します。
今、現在の状態 を
とします。このとき、
を
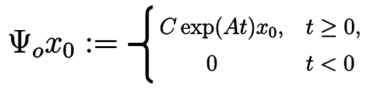
で定義します。線形写像 は
上で入力を
としたときの線形システムの出力値と関係付きます。なぜなら、
が成り立つからです。可制御性グラミアンの時と同様の計算で、
は可観測性グラミアン
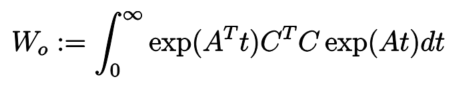
と
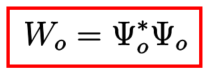
の関係があることが分かります。ここでは、 上に内積を
で定め、ノルムを
で定めることにします。すると、出力は
のため、出力エネルギーが

と可観測性グラミアン を用いて表せることが分かります。可制御性グラミアンの時と同様に、可観測性グラミアン
を用いて定義された集合
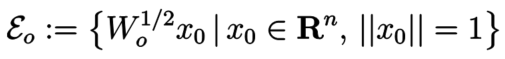
は楕円であり、主軸は の固有ベクトルの方向で、主値は固有値の平方根ということになります。これは球面上の状態
にも「観測のしやすさ 」があり、可観測性グラミアン
の最大固有値に対応する固有ベクトルの方向の状態が最も観測しやすく、最小固有値に対応する固有ベクトルの方向の状態が最も観測しにくいという意味になります。(ここで、観測のしやすさを出力エネルギー
の大小で解釈しています。)
参考文献
記事を書くにあたって次の本を参考にしました。

A Course in Robust Control Theory: A Convex Approach (Texts in Applied Mathematics)
- 作者: Geir E. Dullerud,Fernando Paganini
- 出版社/メーカー: Springer
- 発売日: 2000/02/02
- メディア: ハードカバー
- この商品を含むブログを見る