この記事では線形代数の基本定理とも言われるほど応用上非常に重要な特異値分解について解説します。今はやりのデータサイエンスでもかなり使われています。
対称行列のスペクトル分解
特異値分解は対称行列のスペクトル分解に密接に関係しているので、まずは対称行列のスペクトル分解について説明します。
実数を成分に持つ正方行列 が対称行列だとしましょう。すなわち、
です。このとき、\begin{align} Av_i = \lambda_i v_i \end{align} となる
と
が存在します。ただし、
です。よく知られているように、このような
を
の固有値、
を
の固有値
に対応する固有ベクトルと呼びます。行列
が対称なので、固有ベクトルの集合
を
の正規直交基底とすることができます。いま、\begin{align} V &:= \begin{pmatrix} v_1 & v_2 & \cdots & v_n \end{pmatrix},\quad D:= {\rm diag} (\lambda_1,\lambda_2,\ldots, \lambda_n) \end{align} とすると、\begin{align} A = VDV^T\end{align} となります。右辺の
を対称行列
のスペクトル分解と言います。より詳しくは、以下の記事を参照してください。
特異値分解
次に、 で
でも良い場合を考えてみましょう。正方でない、つまり
の場合は、
の固有値や固有ベクトルを考えることができないので
をスペクトル分解することができません。しかし、
は
に入っているので正方であり、しかも対称行列です。よって、
のスペクトル分解を考えることができます。
対称行列 のスペクトル分解を\begin{align} A^TA = VDV^T\end{align}としましょう。ただし、
は対角行列で対角成分に
の固有値
が並び、
の各列ベクトルは
の固有ベクトル
からなる
の正規直交基底
で構成されているとします。ただし、
とします。このとき、\begin{align} \langle Av_i, Av_j\rangle = \lambda_j \langle v_i, v_j \rangle = \begin{cases} \lambda_i\quad (i=j)\\ 0\quad\,\,\,\,\,\, (i\neq j) \end{cases} \end{align} となります。ただし、
はユークリッド内積です。したがって、
は直交しており、ゼロでないベクトルは
の基底を構成します。また、
とすると\begin{align} ||Av_i||^2 = \lambda_i \end{align} となるので
が分かります。よって、
だとすると、\begin{align} \lambda_i = 0\quad (k<i\leq n)\end{align} となります。したがって、\begin{align} u_i:= \frac{Av_i}{||Av_i||} = \frac{1}{\sqrt{\lambda_i}} Av_i\quad (1\leq i\leq k) \end{align} は
の正規直交基底を構成します。もし、
の場合は、この正規直交基底を
の正規直交基底へ延長することもできます。実際に、この正規直交基底をなすベクトル
に一次独立な
個のベクトルをもってきて次の記事で解説したグラム・シュミットの直交化法を利用することで
の正規直交基底
を作ることができます。
以上より、\begin{align} Av_i &= \sigma_i u_i\quad (1\leq i\leq k)\\ Av_i &=0\quad\,\,\,\,\,\, (k<i\leq n) \end{align} となります。ただし、 です。このことより、
を用いると(作り方から
であることに注意)、行列
は\begin{align} A=U\Sigma V^T \end{align} と分解できることが分かります。ただし、\begin{align} U:=\begin{pmatrix} u_1 & u_2 & \cdots & u_m \end{pmatrix}\end{align} で
は
の正規直交基底です。この
を
の特異値分解、
を
の特異値、
の各列を左特異ベクトル、
の各列を右特異ベクトルと言います。特異値分解は、以下のように任意の行列による写像が回転や拡大の写像に分解できることを意味しています。

また、特異値分解は\begin{align} A= \sum_{i=1}^k \sigma_i u_i v_i^T \end{align} というように、 個分だけランク1の行列を加算することを意味します。この表現を用いると、任意の
に対して\begin{align} Ax = \sigma_1x_1u_1+\sigma_2x_2u_2+\cdots +\sigma_k x_k u_k \end{align}が成り立つことが分かります。特に、
なら\begin{align} Ax = \sigma_1u_1+\sigma_2u_2+\cdots +\sigma_k u_k \end{align}となります。このことを
の
に対して可視化したのが上の図です。
行列の作用素ノルム
任意の に対して\begin{align} ||A||:= \max_{x\in {\bf R}^n\backslash\{0\}} \frac{||Ax||}{||x||} = \max_{||x||=1} ||Ax|| \end{align}とすると
はノルムとなります。このノルムを作用素ノルムと言います。以下のように、行列
の作用素ノルムは最大特異値になります。


例えば、 となる任意の
の作用素ノルムは
になります。なぜなら、任意の
に対して\begin{align} ||Ux||^2=x^TU^TUx=||x||^2 \end{align} が成り立つからです。また、サイズの異なる行列
に対して\begin{align} ||AB||\leq ||A||\cdot ||B|| \end{align}が成り立ちます。なぜなら、任意の
に対して\begin{align} ||ABx||\leq ||A||\cdot ||Bx||\leq ||A||\cdot ||B||\cdot ||x|| \end{align} が成り立つからです。さらに、以下が成り立ちます。

証明は以下の通りです。

行列の低ランク近似
与えられた行列 の最適な近似が特異値分解を利用することで以下のように得られます。この結果はエッカート・ヤング(Eckart-Young)の定理と言われています。

証明は以下の通りです。

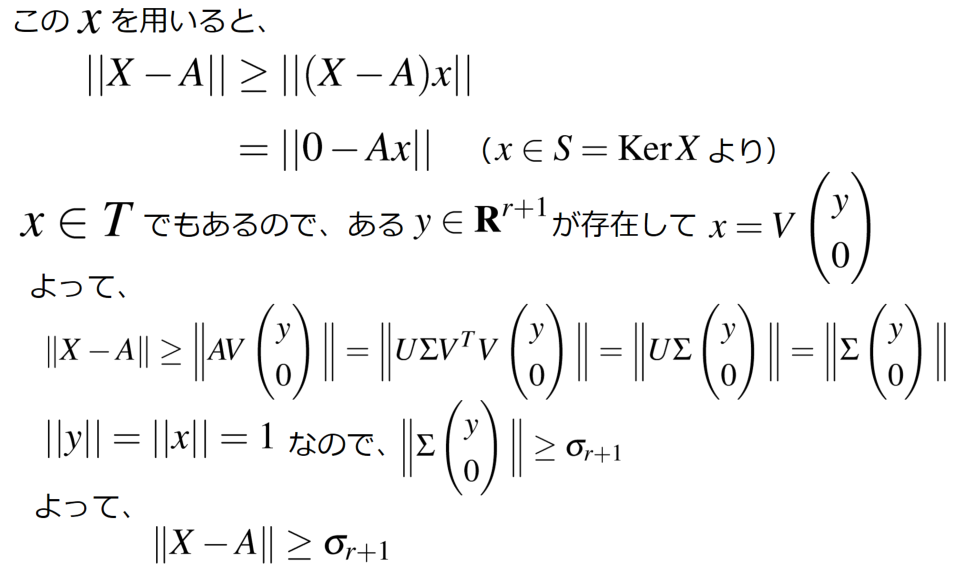
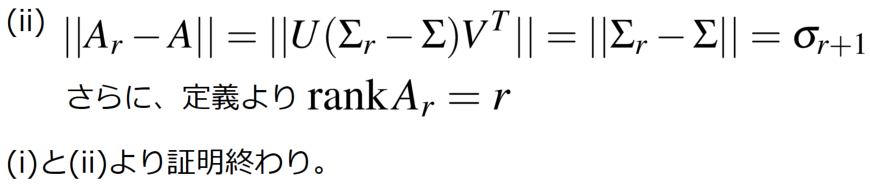
この定理は以下を意味します。
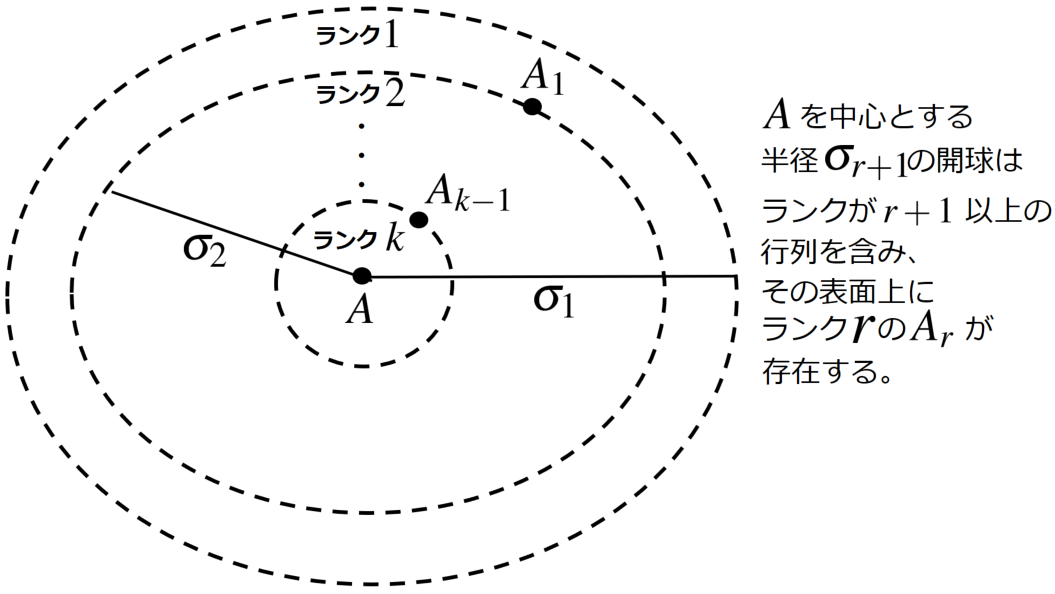
この定理は行列 のランクを
だとしたときに、ランク
以下で
に最も近い行列が
自身を特異値分解することで得られることを示しており、このことから特異値分解が応用上非常に重要だということになります。例えばデータサイエンスの文脈では、
はデータを格納した行列ということが多いですが、この
のサイズが非常に大きい(
が非常に大きい)と情報処理が大変になります。このようなときに、
を特異値分解して、
に最も近い低ランクな行列を構成する特異値と特異ベクトルを抽出しておけば、データ処理が非常に簡単になります。
参考文献
この記事を書くにあたって参考にした文献です。

Approximation of Large-Scale Dynamical Systems (Advances in Design and Control)
- 作者:Athanasios C. Antoulas
- 出版社/メーカー: Society for Industrial and Applied Mathematics
- 発売日: 2009/06/25
- メディア: ペーパーバック

