伝達関数 - 初級Mathマニアの寝言

この記事では線形システムの制御で重要な役割を果たす伝達関数について説明します。

●ラプラス変換

伝達関数を理解するためには関数のラプラス変換を知っている必要があります。ラプラス変換は次のように定義されます。

f:id:ogyahogya:20151024152142p:plain

上のラプラス変換は前の記事で説明したフーリエ変換に似ていますが、次のような違いがあります。

f:id:ogyahogya:20151027174428p:plain

ogyahogya.hatenablog.com

●伝達関数

線形システムの伝達関数は次のように入力関数のラプラス変換と出力関数のラプラス変換の比で定義されます。

f:id:ogyahogya:20151024153012p:plain

伝達関数は次のように座標変換のもとで不変です。

f:id:ogyahogya:20151024153121p:plain

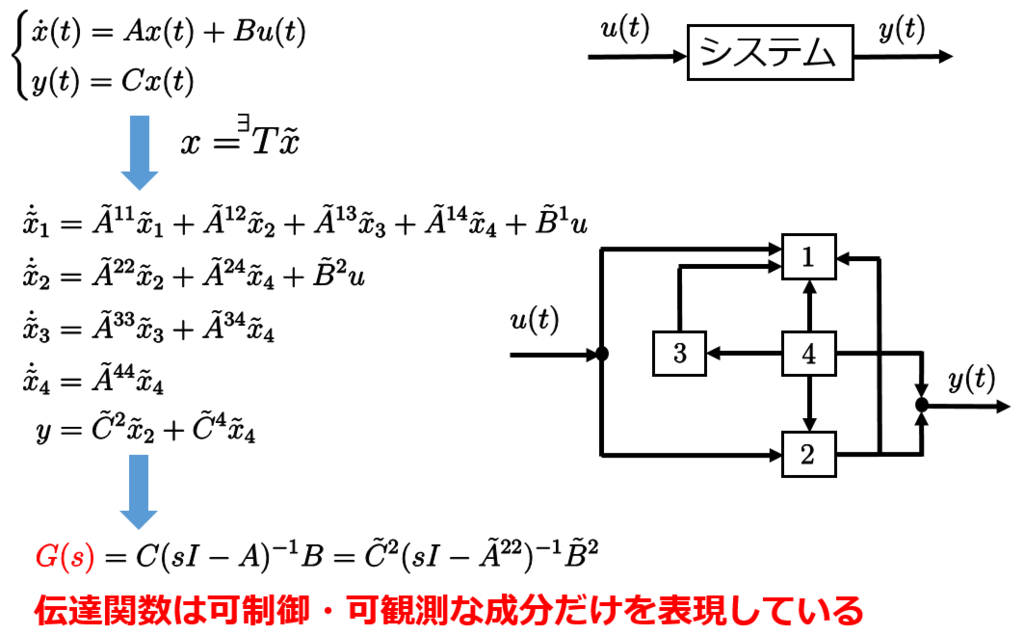
●伝達関数と可制御性・可観測性

伝達関数の概念と前の記事で説明した可制御性と可観測性の概念は次のように結びつきます。

f:id:ogyahogya:20151024154914p:plain

ogyahogya.hatenablog.com

●伝達関数とインパルス応答行列

線形システムの入力としてインパルスというディラックのデルタ関数を加えたときの出力と伝達関数は次のように結びつきます。

f:id:ogyahogya:20151024155714p:plain

ディラックのデルタ関数については前の記事で詳しく説明しましたので興味のある人は見てください。

ogyahogya.hatenablog.com

●周波数応答

上の議論よりインパルス応答行列のラプラス変換が伝達関数なわけですが、次のようにインパルス応答行列のフーリエ変換を周波数応答行列と言います。

f:id:ogyahogya:20151024161418p:plain

周波数応答行列と伝達関数の間には次のような関係があります。

f:id:ogyahogya:20151024161521p:plain

1入力1出力の周波数応答行列は周波数応答関数と呼ばれます。周波数応答関数が分かると過渡応答が分かるため制御工学では周波数応答関数を理解するが大事です。周波数応答関数を図的に理解する方法として、ナイキスト線図やボード線図と呼ばれるものがあります。ナイキスト線図やボード線図については制御工学の本を見てください。

●伝達関数の $H^2$ ノルム

線形システムの $A$ 行列が安定、つまり、 $A$ のすべての固有値の実部が負のときに

f:id:ogyahogya:20151024163532p:plain

が定義できて、これを伝達関数 $G$ の $H^2$ ノルムと言います。前の記事で説明したプランシュレルの定理（パーセバルの等式ともいう）より

f:id:ogyahogya:20151024163650p:plain

となります。さらに

f:id:ogyahogya:20151024163818p:plain

なので

f:id:ogyahogya:20151024163840p:plain

となることが分かります。つまり、制御する側からすると $||G||_2$ は小さいほど嬉しいわけです。

伝達関数の $H^2$ ノルムを定義通り計算しようとすると無限区間の積分を計算しなければならず、面倒です。しかし、 $H^2$ ノルムは定義通りに計算する必要はなく、以下のように容易に計算できます。まず、インパルス応答行列 $g(t)$ を $||G||_2$ の中へ代入すると次のようになります。

f:id:ogyahogya:20151024165233p:plain

さらに、

f:id:ogyahogya:20151024165403p:plain

が成り立つことに注意すると、

f:id:ogyahogya:20151024165425p:plain

が成り立つことが分かります。上の $W_c$ や $W_o$ に関する線形行列方程式はリヤプノフ方程式と呼ばれており、解は上のように積分の形で具体的に表示できるのですが、実際には積分を計算せずに他の解法アルゴリズムを用いて数値的に求めます。例えば、有名な計算ソフトフェアであるMatlabにはリヤプノフ方程式を解くlyapというコマンドが用意されていますが、その解法は積分を計算していません。