この記事では多様体上の接続と平行移動という概念について解説します。なお、この記事を理解するためには多様体、接空間、ベクトル場といった概念を理解しておく必要がありますが、それらについては以下の記事を参考にしてください。
- 多様体上のアファイン接続
- ユークリッド空間の場合の共変微分
- ユークリッド空間の部分多様体の場合の共変微分
- 具体例
- ユークリッド空間の部分多様体の場合における平行と平行移動の概念
- 一般の多様体の場合の平行と平行移動の概念
- 参考文献
多様体上のアファイン接続
多様体上のアファイン接続という概念は多様体上の異なる2点の接空間を関係付ける(つなげる)概念であり、以下のように定義されます。

ここで、 は
上の滑らかなベクトル場全体の集合です。定義の(i)と(ii)から
は
について
-線形で、(iii)と(iv)から
は
について
-線形であることが分かります。また、(ii)は
がライプニッツ則を満たすことを意味しています。
アファイン接続の定義はかなり抽象的であるため、異なる接空間のつながり方を定めていることがイメージしにくいと思います。そこで、以下で詳しくアファイン接続が接空間をつなげている様子を見ていきたいと思います。そのために、まず共変微分が具体的には何なのかを考えます。
ユークリッド空間の場合の共変微分
まず、多様体がユークリッド空間の場合には、方向微分は共変微分になることを説明します。
多様体 がユークリッド空間
の場合を考えましょう。ユークリッド空間
上の任意の滑らかなベクトル場
が与えられているとします。このとき、
の点
での
に沿った方向微分(ガトー微分)とは、
で紹介したように、\begin{align} ({\rm D}_X Y)(p):={\rm D}_{X(p)} Y(p) = \lim_{t\rightarrow 0} \frac{Y(p+tX(p)) -Y(p)}{t} \end{align} のことです。ベクトル場のベクトル場に沿った方向微分は共変微分と同じ形をしている以下の性質を満たします。
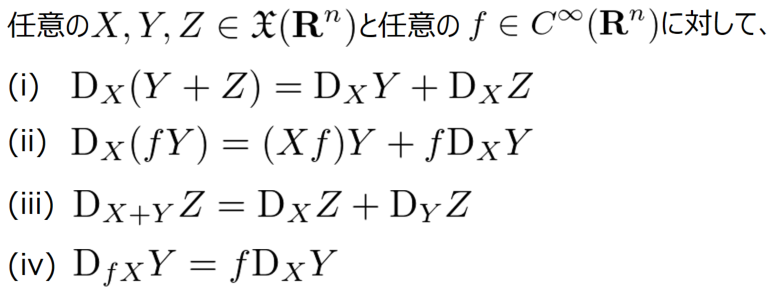
方向微分が上の性質を満たすことの証明はどれも簡単ですが、(ii) と (iii) を証明しておきます。まず (ii) の証明をします。任意の に対して \begin{align} ({\rm D}_X (fY))(p) = \lim_{t\rightarrow 0} \frac{ (fY)(p+tX(p)) -(fY)(p)}{t} \end{align} が成り立ちますが、右辺は \begin{align} \lim_{t\rightarrow 0} \frac{ f(p+tX(p))Y(p+tX(p)) -f(p)Y(p+tX(p))}{t} + \lim_{t\rightarrow 0} \frac{f(p)Y(p+tX(p)) -f(p)Y(p)}{t} \end{align} のことですので (ii) が成り立ちます。次に (iii) の証明をします。 ベクトル場
は滑らかなのでガトー微分とフレッシェ微分が一致して \begin{align} {\rm D}_X Z(p) = {\rm D} Z(p)[X(p)] \end{align} が成り立ちます。フレッシェ微分 (ここでは普通のヤコビ行列)
は線形ですので、 \begin{align} {\rm D}_{X+Y} Z(p) = {\rm D} Z(p) [X(p)+Y(p)] = {\rm D} Z(p)[X(p)] + {\rm D} Z(p)[Y(p)] = {\rm D}_X Z(p) + {\rm D}_Y Z(p) \end{align} となるので (iii) が成り立ちます。
任意の に対して方向微分
も
の要素となるので、多様体
がユークリッド空間の場合は方向微分は共変微分になっているということが確認できました。つまり、ユークリッド空間の場合は方向微分によってアファイン接続が定義できるということです。
ユークリッド空間の部分多様体の場合の共変微分
次に、多様体がユークリッド空間の部分多様体の場合には、方向微分は共変微分にならず、方向微分の接空間への射影が共変微分になることを説明します。
局所座標を使わない説明
上と同じように多様体 で任意の滑らかなベクトル場
が与えられているとします。そして、
をユークリッド空間
の部分多様体だとします。ベクトル場
は
上で与えられていますが、
上に制限して
だとも考えることができます。このとき
の
に沿った方向微分
は
に入っているでしょうか? 一般には入っていません。つまり、
は多様体
の点
での接空間
の要素ですが、
は接空間
の要素にはなっていないことがあります。これは、
は言えますが、
は言えないということです。
なら
が言えないので
を共変微分とは言えないということになります。
しかし、 と直交直和分解すると、
を \begin{align} {\rm D}_X Y(p) = {\rm P}_p ({\rm D}_X Y(p)) + {\rm P}^{\perp}_p({\rm D}_X Y(p)) \end{align} と一意に分解することができます。ここで、\begin{align} {\rm P}_p: T_p {\bf R}^n \rightarrow T_p U \end{align} は射影です。この事実を利用して\begin{align} \nabla_X Y(p):={\rm P}_p ({\rm D}_X Y(p)) \end{align} と
を定義すると
は共変微分の性質 (i)~(iv) を満たします。つまり、方向微分の接空間への射影は共変微分になり、これによってアファイン接続が定義できました。ここまでの議論を図示すると以下のような感じです。

局所座標と曲線を使った説明
次に、多様体がユークリッド空間の部分多様体の場合で、ユークリッド空間上のベクトル場を与えられた曲線から定められる速度ベクトル場に沿った方向微分は共変微分には一般にはならないことを局所座標を用いて確認します。
多様体 と任意の滑らかなベクトル場
を考えます。そして、
をユークリッド空間
の
次元の部分多様体だとして、
上の曲線
が与えられているとします。
曲線 は局所座標
を用いて
と書けます。部分多様体
の曲線
上ではベクトル場
と速度ベクトル場
は \begin{align} X(c(t)) &= \sum_{i=1}^m f_i(x_1(t),x_2(t),\ldots, x_m(t)) \left( \frac{\partial}{\partial x_i}\right)_{c(t)} \\ \dot{c}(t) &= \sum_{i=1}^m \dot{x}_i(t) \left(\frac{\partial}{\partial x_i}\right)_{c(t)} \end{align} と書けます。つまり、
です。
これからベクトル場 を曲線の速度ベクトル場
に沿って方向微分します。ここで、
は曲線
上の滑らかなベクトル場全体の集合です。曲線
上では
になることを注意してください。ベクトル場のベクトル場に沿った方向微分の性質 (i)~(iv) を用いると方向微分
は以下のように計算できます。
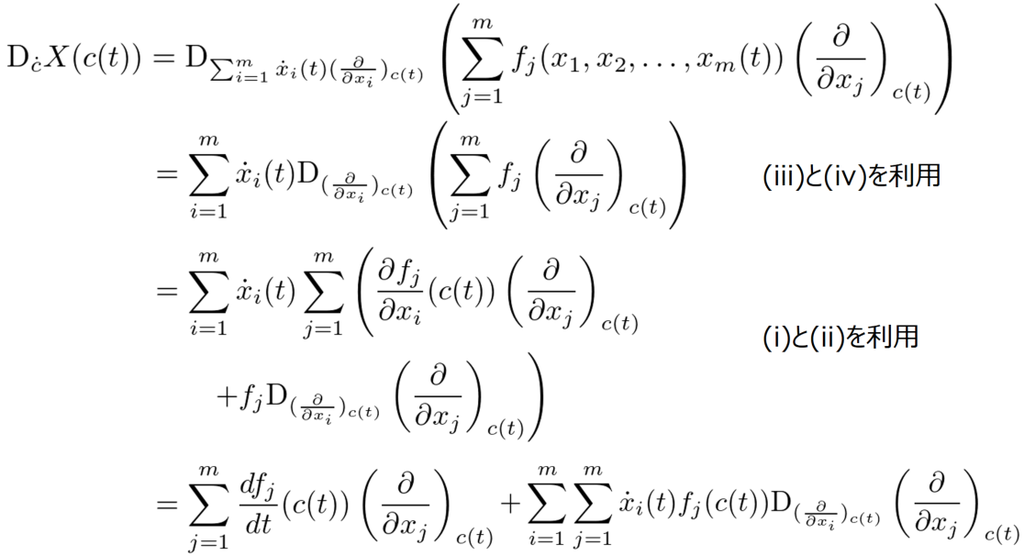

さらに、 がベクトル場
の積分曲線、つまり
だとすると、上の計算結果より\begin{align} {\rm D}_{\dot{c}} \dot{c}(c(t)) = \sum_{j=1}^m \ddot{x}_j(t) \left( \frac{\partial}{\partial x_j}\right)_{c(t)} + \sum_{i=1}^m \sum_{j=1}^m \dot{x}_i(t)\dot{x}_j(t) {\rm D}_{(\frac{\partial}{\partial x_i})_{c(t)}}\left( \frac{\partial}{\partial x_j}\right)_{c(t)} \end{align}が得られます。以下の具体例で具体的に見るように、この
は局所座標を用いた曲線の2回微分
、つまり加速度ベクトルに等しいです。したがって曲線
の速度ベクトル
は
に入っていますが、加速度ベクトル
は一般には
に入っていないということが分かりました。
具体例
ここまでの内容を具体的に見てみます。例として、多様体 を以下の単位球面とします。この球面の上半分を局所座標
を用いてパラメータ表示します。

この球面上に曲線 があり、この曲線に沿ったベクトル場
があるとします。このとき、ベクトル場
を同じベクトル場
に沿って共変微分するとどうなるか具体的に見てみます。
そのために、まず点 での接ベクトル
が\begin{align} \dot{c}(t) = \dot{x}_1(t) \left(\frac{\partial}{\partial x_1}\right)_{c(t)} + \dot{x}_2(t) \left(\frac{\partial}{\partial x_2}\right) _{c(t)} \end{align} と書けたことを思い出しましょう。つまり、接空間
は \begin{align} T_{c(t)} M={\rm span}\, \{\left(\frac{\partial}{\partial x_1}\right)_{c(t)}, \left(\frac{\partial}{\partial x_2}\right)_{c(t)} \} \end{align} と書けました。しかし、
という書き方は接ベクトルの微分作用素としての側面を強調した書き方のため分かりにくいかもしれません。接ベクトルを矢印のベクトルとして理解するために、
と
の2次元の部分空間を同一視して考えましょう。つまり、
を2次元のユークリッド空間だと考えましょう。
具体的には以下のように を2次元のユークリッド空間だと考えることができます。上の図で示した写像
を用いて曲線
を\begin{align} c(t) = q(x_1(t),x_2(t))=q(x(t)) \end{align} と書きます。そうすると、接ベクトル
は\begin{align} \dot{c}(t) = \dot{x}_1(t)\frac{\partial q}{\partial x_1}(x(t))+\dot{x}_2(t)\frac{\partial q}{\partial x_2}(x(t)) \end{align} となります。ここで、\begin{align} \frac{\partial q}{\partial x_1}(x(t)) = \begin{pmatrix} 1 \\ 0 \\ -\frac{x_1(t)}{\sqrt{1-x_1^2(t)-x_2^2(t)}} \end{pmatrix}, \,\,\,\, \frac{\partial q}{\partial x_2}(x(t)) = \begin{pmatrix} 0 \\ 1 \\ -\frac{x_2(t)}{\sqrt{1-x_1^2(t)-x_2^2(t)}} \end{pmatrix} \end{align} です。したがって、
を2次元のユークリッド空間だと考えてるということは
を
と同一視するということを意味しています。
さらに、接ベクトル を
について微分して加速度ベクトル
を計算すると以下のようになります。\begin{align} \ddot{c}(t) = \sum_{i=1}^2 \left( \ddot{x}_i(t) \frac{\partial q}{\partial x_i}(x(t))+\dot{x}^2_i(t)\frac{\partial^2 q}{\partial x_i^2}(x(t)) \right) +2\dot{x}_1(t)\dot{x}_2(t)\frac{\partial^2 q}{\partial x_1\partial x_2}(x(t)) \end{align}ここで、
なので、\begin{align} \ddot{c}(t) = {\rm D}_{\dot{c}}\dot{c}(c(t)) \end{align} となることを確認できました。
もっと詳しく加速度ベクトル を調べます。表記を簡単にするために、
と書いて、
と
と
の外積によって
を定義すると、
は
の基底ベクトルになるため \begin{align} \frac{\partial^2 q}{\partial x_i \partial x_j}(x(t)) = \Gamma^1_{ij}(x(t))q_1(x(t))+\Gamma^2_{ij}(x(t))q_2(x(t)) + v_{ij} e \end{align} と書くことができます。ここで、
なので
が成り立ちます。したがって、加速度ベクトルは \begin{align} \ddot{c}(t) =& \sum_{i=1}^2(\ddot{x}_i(t) + \dot{x}_1^2(t) \Gamma_{11}^i + 2\dot{x}_1(t)\dot{x}_2(t) \Gamma_{12}^i + \dot{x}_2^2(t) \Gamma_{22}^i) q_i\\ &+ (\dot{x}_1^2(t)v_{11} + 2\dot{x}_1(t) \dot{x}_2(t)v_{12} + \dot{x}_2^2(t) v_{22} ) e \end{align} となります。この式から一般には加速度ベクトル
には
方向の成分があることが分かります。よって、ベクトル
の定義から
と
は直交しているため、
の成分がゼロにならない限り
は接空間
からはみ出るということを意味しています。
加速度ベクトル の
の成分がゼロになると実は
は接空間
の要素だということになりますが、一般にはならないことを念のため数値的に確認します。まず、
なので \begin{align} e = \begin{pmatrix} \frac{x_1(t)}{\sqrt{1-x_1^2(t)-x_2^2(t)}} \\ \frac{x_2(t)}{\sqrt{1-x_1^2(t)-x_2^2(t)}} \\ 1 \end{pmatrix} \end{align} となります。また、\begin{align} \frac{\partial^2 q}{\partial x_1^2} = \begin{pmatrix} 0 \\ 0 \\ \frac{x_2^2-1}{(1-x_1^2-x_2^2)^{3/2}} \end{pmatrix},\,\, \frac{\partial^2 q}{\partial x_2^2} = \begin{pmatrix} 0 \\ 0 \\ \frac{x_1^2-1}{(1-x_1^2-x_2^2)^{3/2}} \end{pmatrix},\,\, \frac{\partial^2 q}{\partial x_1 \partial x_2} = \begin{pmatrix} 0 \\ 0 \\ -\frac{x_1x_2}{(1-x_1^2-x_2^2)^{3/2}} \end{pmatrix} \end{align}となります。したがって、\begin{align} \frac{\partial^2 q}{\partial x_1^2} &= \frac{x_1(1-x_2^2)}{1-x_1^2-x_2^2}q_1 + \frac{x_2(1-x_2^2)}{1-x_1^2-x_2^2}q_2 -\frac{1-x_2^2}{\sqrt{1-x_1^2-x_2^2}}e \\ \frac{\partial^2 q}{\partial x_2^2} &= \frac{x_1(1-x_1^2)}{1-x_1^2-x_2^2}q_1 + \frac{x_2(1-x_1^2)}{1-x_1^2-x_2^2}q_2 -\frac{1-x_1^2}{\sqrt{1-x_1^2-x_2^2}}e \\ \frac{\partial^2 q}{\partial x_1 \partial x_2} &= \frac{x_1^2 x_2}{1-x_1^2-x_2^2}q_1 + \frac{x_1x_2^2}{1-x_1^2-x_2^2}q_2 -\frac{x_1x_2}{\sqrt{1-x_1^2-x_2^2}}e \end{align}です。よって、
のとき、\begin{align} \frac{\partial^2 q}{\partial x_1^2} &= \frac{2}{3}q_1 -\frac{2\sqrt{3}}{3}e \\ \frac{\partial^2 q}{\partial x_2^2} &= \frac{1}{2}q_1 -\frac{\sqrt{3}}{2}e \end{align} となって、\begin{align} \Gamma_{11}^1 = \frac{1}{2},\,\, \Gamma_{11}^2 = 0,\,\, \Gamma_{22}^1= \frac{1}{2},\,\, \Gamma_{22}^2 = 0,\,\, \Gamma_{12}^1=\Gamma_{12}^2=0,\,\, v_{11}= -\frac{2\sqrt{3}}{3},\,\, v_{22} = -\frac{\sqrt{3}}{2},\,\, v_{12} = 0 \end{align} が得られます。つまり、加速度ベクトル
の
成分は \begin{align} -\frac{2\sqrt{3}}{3} \dot{x}_1^2(t) -\frac{\sqrt{3}}{2}\dot{x}_2^2(t) \end{align} となって、
でない限り
成分はゼロにならないことが分かりました。これは一般には
であることを意味しています。
ユークリッド空間の部分多様体の場合における平行と平行移動の概念
上の説明よりユークリッド空間 上のベクトル場
を
次元部分多様体
上の曲線
の速度ベクトル場
に沿って方向微分すると\begin{align} {\rm D}_{\dot{c}}X(c(t)) \not\in T_{c(t)} M \end{align} でした。そこで、上で説明した射影
を用いて\begin{align} \nabla_{\dot{c}(t)} X(c(t)) := {\rm P}_{c(t)} ( {\rm D}_{\dot{c}} X(c(t)) ) \end{align} を定義します。すると、
はアファイン接続となります。射影
は線形なので\begin{align} \nabla_{\dot{c}} X(c(t)) &= \sum_{j=1}^m \frac{df_j}{dt}(c(t)) \left( \frac{\partial}{\partial x_j}\right)_{c(t)} + \sum_{i=1}^m \sum_{j=1}^m \dot{x}_i(t) f_j(t) {\rm P}_{c(t)} \left({\rm D}_{(\frac{\partial}{\partial x_i})_{c(t)}}\left( \frac{\partial}{\partial x_j}\right)_{c(t)}\right) \\ &= \sum_{j=1}^m \frac{df_j}{dt}(c(t)) \left( \frac{\partial}{\partial x_j}\right)_{c(t)} + \sum_{i=1}^m \sum_{j=1}^m \dot{x}_i(t) f_j(t) \nabla_{(\frac{\partial}{\partial x_i})_{c(t)}}\left( \frac{\partial}{\partial x_j}\right)_{c(t)} \end{align} となります。ただし、
です。さらに、ある滑らかな関数
を用いて\begin{align} \nabla_{(\frac{\partial}{\partial x_i})_{c(t)}}\left( \frac{\partial}{\partial x_j}\right)_{c(t)} = \sum_{k=1}^m \Gamma_{ij}^k(c(t)) \left( \frac{\partial}{\partial x_k}\right)_{c(t)} \end{align}と書けますので、\begin{align} \nabla_{\dot{c}} X(c(t)) = \sum_{k=1}^m \left( \frac{df_k}{dt}(c(t)) + \sum_{i=1}^m \sum_{j=1}^m \Gamma_{ij}^k(c(t)) \dot{x}_i(t) f_j(t) \right) \left( \frac{\partial}{\partial x_k}\right)_{c(t)} \end{align}となります。これがゼロになるとき、つまり、\begin{align} \nabla_{\dot{c}} X(c(t)) = 0 \end{align} が成り立つときにベクトル場
がアファイン接続
に関して曲線
に沿って平行であると言います。また、
は\begin{align} \frac{df_k}{dt}(c(t)) + \sum_{i=1}^m \sum_{j=1}^m \Gamma_{ij}^k(c(t)) \dot{x}_i(t) f_j(t)=0 \quad (k=1,2,\ldots, m) \end{align} のことであることに注意しましょう。ただし、
で
です。この微分方程式は\begin{align}\frac{d}{dt} \begin{pmatrix} f_1 \\ \vdots \\ f_m \end{pmatrix} = -
\begin{pmatrix} \sum_{i=1}^m\Gamma_{i1}^1\dot{x}_i & \cdots & \sum_{i=1}^m\Gamma_{im}^1\dot{x}_i \\ \vdots & & \vdots \\ \sum_{i=1}^m\Gamma_{i1}^m\dot{x}_i & \cdots & \sum_{i=1}^m\Gamma_{im}^m\dot{x}_i \end{pmatrix}\begin{pmatrix} f_1 \\ \vdots \\ f_m \end{pmatrix} \end{align} と書けるのでベクトル場 の成分
に関して線形の微分方程式となっていることが分かります。したがって、点
における接ベクトル
を任意に与えると、曲線
に沿って平行なベクトル場であって、
を満たすものが、初期条件
のもとでの上の線形微分方程式の解として一意に定まります。このようにして定まる
を曲線
に沿って
を
から
まで平行移動して得られる接ベクトルと言います。
このように平行と平行移動の概念が定義されました。しかし、この定義を満たしたときに平行と呼ぶ理由や、平行の定義に曲線が登場する理由は自明ではないと思います。そこで以下では、これらの理由を説明します。
平行の名前の由来
以下では、 が成り立つときに平行と呼ぶ理由を調べます。まず、2次元ユークリッド空間
の場合では以下のことが成り立つときに(
が成り立つかは知らなかったとしても)ベクトル場を平行と呼ぶことを自然に感じる人が多いと思います。

上と同じベクトル場 に加えて曲線
が与えられたすると、次のようにベクトル場
はアファイン接続
(この場合は通常の方向微分から定義される)に関し曲線
に沿って平行、つまり
であることが分かります。

このようにユークリッド空間に直交座標系を入れて考える場合、各点から出る矢印ベクトルがすべて同じ大きさと向きを持つようなベクトル場 は曲線
が与えられたときに
を満たします。
では、ユークリッド空間に直交座標系 ではない以下のような曲線座標系
を導入したらどうなるでしょうか?
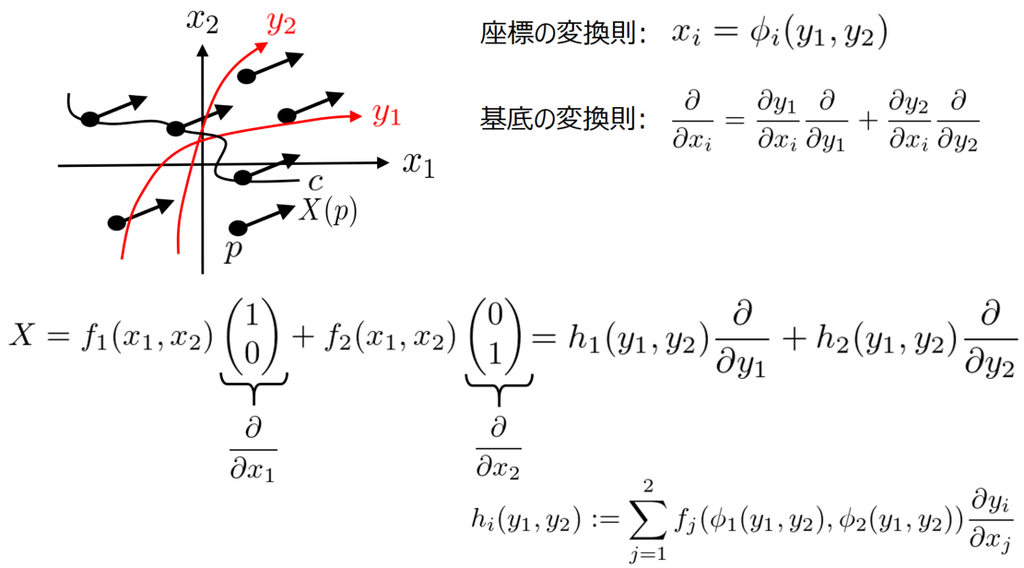
共変微分(方向微分)の結果が座標に依存するようでは困るので、直交座標系 のときに
だったら曲線座標系
の場合でも
と言いたいです。では、どのように曲線座標系
の場合でも
だと言えるのでしょうか?直交座標系
の場合は
と
から
が言えました。曲線座標系
の場合でも
と
から言えるのでしょうか?一般にはそのようには言えませんが、
を曲線座標系
で表現したときの
の成分と
の成分がゼロになることから言えるということになります。つまり、曲線座標系
の場合ではベクトル場
がアファイン接続
に関し曲線
に沿って平行であるというのは \begin{align} \frac{dh_k}{dt}(y_1(t),y_2(t)) + \sum_{i=1}^2 \sum_{j=1}^2 \Gamma_{ij}^k(y_1(t),y_2(t))\dot{y}_i(t) h_j(t) = 0\quad (k=1,2) \end{align} が成り立つときに言います。直交座標系を使うと
がゼロになりましたが、曲線座標系を使うとゼロにならなくなってしまうことからベクトル場が平行だということを上の微分方程式を満たすときに言おうということになります。なぜかというと、このときに直交座標系の場合と同様に
になるからです。
曲線の重要性
ここでは、平行の概念を論じる際にはどの曲線を考えているかが重要であることを多様体 が以下の単位球の場合に説明します。
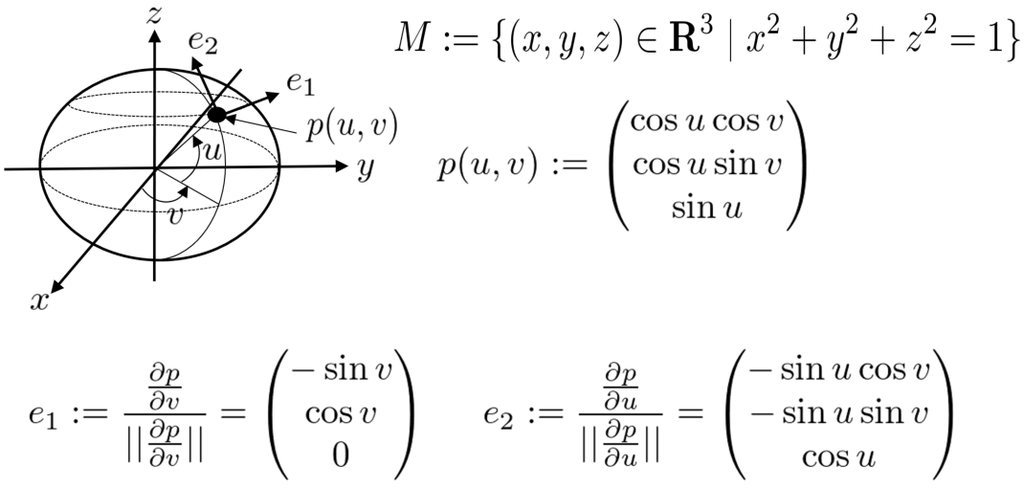
ただし、\begin{align} \frac{\partial p}{\partial v} = \begin{pmatrix} -\cos u \sin v \\ \cos u \cos v \\ 0 \end{pmatrix} \end{align} なので \begin{align} -\frac{\pi}{2}< u < \frac{\pi}{2},\quad -\pi \leq v \leq \pi \end{align} とします。
このとき、 となる
上の任意の滑らかなベクトル場
は\begin{align} X(u,v) = f_1(u,v)e_1+ f_2(u,v)e_2 \end{align} と書けます。また、
上に曲線
があるとすると、この曲線に関する速度ベクトル場は\begin{align} \dot{c} = \dot{u}(t)\frac{\partial}{\partial u} + \dot{v}(t) \frac{\partial}{\partial v} \end{align} となります。共変微分として方向微分の接空間への射影を採用してアファイン接続
を定めます。そうすると、ベクトル場
がアファイン接続
に関して曲線
に沿って平行である、つまり、
は\begin{align} \frac{d}{dt}\begin{pmatrix} f_1 \\ f_2 \end{pmatrix} = \begin{pmatrix} 0 & \dot{v} \sin u \\ -\dot{v}\sin u & 0 \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \end{pmatrix} \end{align}ということになります。
いま、 を定数で
とすると、
なので上の微分方程式の解は\begin{align}\begin{cases} f_1(u(t),v(t)) = \cos (\lambda t)f_1(u(0),v(0)) +\sin (\lambda t) f_2(u(0),v(0)) \\ f_2(u(t),v(t)) = -\sin(\lambda t) f_1(u(0),v(0)) + \cos (\lambda t) f_2(u(0),v(0)) \end{cases} \end{align} となります。ただし、
です。よって、
のとき\begin{align} \begin{cases} f_1(u(\pi),v(\pi)) = \cos (\lambda \pi) \\ f_2(u(\pi),v(\pi)) = -\sin(\lambda \pi) \end{cases} \end{align} となります。つまり、時刻
で\begin{align} X(u(0),v(0))= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix} \end{align} のベクトルが時刻
で \begin{align} X_1:= X(u(\pi),v(\pi))= \cos (\lambda \pi)\begin{pmatrix} 0 \\ -1\\ 0 \end{pmatrix} -\sin(\lambda \pi) \begin{pmatrix} \sin \alpha \\ 0 \\ \cos \alpha \end{pmatrix} \end{align}
となります。このベクトル は点
のベクトル
を曲線
に沿って点
まで平行移動したベクトルとなっていることに注意してください。
同様に、 を定数で
とすると、 時刻
で\begin{align} X(u(0),v(0))= \begin{pmatrix} 0 \\ 1\\ 0 \end{pmatrix} \end{align} のベクトルが時刻
で \begin{align} X_2:=X(u(\pi),v(\pi))= \cos (\lambda \pi)\begin{pmatrix} 0 \\ -1\\ 0 \end{pmatrix} +\sin(\lambda \pi) \begin{pmatrix} \sin \alpha \\ 0 \\ \cos \alpha \end{pmatrix} \end{align}となることが分かります。このベクトル
は点
のベクトル
を曲線
に沿って点
まで平行移動したベクトルとなっています。
上の二つのベクトル と
は
なら異なりますが、\begin{align} p(\alpha,\pi)=p(\alpha,-\pi) = \begin{pmatrix} -\cos \alpha\\ 0 \\ \sin \alpha \end{pmatrix} \end{align} となっており、
と
は同じ点のベクトルとなっています。しかも、この二つのベクトルは両方とも点
のベクトル
を平行移動して得られたベクトルでした。違いは、どの曲線に沿って平行移動したかだけです。
このように、同じ場所の同一のベクトルを異なる曲線に沿って平行移動すると、以下の図のような感じで一般には異なるベクトルが得られるので曲線を使って平行の概念を定義します。
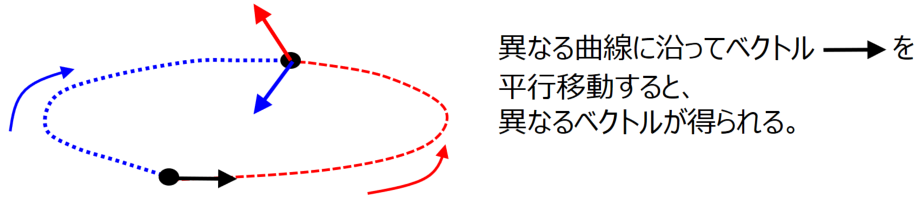
一般の多様体の場合の平行と平行移動の概念
ここまでの話は多様体 をユークリッド空間の部分多様体としてきました。つまり、多様体
の外の世界もあるとしてきました。外の世界も考えていたので多様体の接空間からはみ出たベクトルを射影して接空間に落とすということも考えることができました。
以下では多様体 の外の世界は考えないで説明します。つまり、アファイン接続は定義の(i)~(iv)を満たす抽象的な写像のことであり、部分多様体のときの場合のように「方向微分の射影」から定義されません。しかし、抽象的なままでは分かりにくいので部分多様体の場合をイメージしながら理解すれば良いかと思います(多様体がユークリッド空間の部分多様体の場合にも以下の議論は成り立ちますし、応用上はユークリッド空間の部分多様体を考える場合の方が多いと思われますので)。
次元の多様体
にアファイン接続
が定義されているとします。このとき、多様体
の座標近傍
で \begin{align} \nabla_{\frac{\partial}{\partial x_i}} \frac{\partial}{\partial x_j} = \sum_{k=1}^m\Gamma_{ij}^k \frac{\partial}{\partial x_k} \end{align} で定まる
個の滑らかな関数
を局所座標系
に関する接続係数と言います。
多様体 上の滑らかな曲線
に沿って定義されたベクトル場
が\begin{align} \nabla_{\dot{c}}X(c(t))=0 \end{align} を満たすとき、
はアファイン接続
に関して
に沿って平行であると言います。これは、多様体
がユークリッド空間の部分多様体の場合の平行の定義と一致しています。 座標近傍
上で
を局所座標表示すると、
が部分多様体の場合のときと同様に、\begin{align} \frac{df_k}{dt}(c(t)) + \sum_{i=1}^m \sum_{j=1}^m \Gamma_{ij}^k(c(t)) \dot{x}_i(t) f_j(t)=0 \quad (k=1,2,\ldots, m) \end{align} となります。ただし、
で
です。この微分方程式は\begin{align}\frac{d}{dt} \begin{pmatrix} f_1 \\ \vdots \\ f_m \end{pmatrix} = -
\begin{pmatrix} \sum_{i=1}^m\Gamma_{i1}^1\dot{x}_i & \cdots & \sum_{i=1}^m\Gamma_{im}^1\dot{x}_i \\ \vdots & & \vdots \\ \sum_{i=1}^m\Gamma_{i1}^m\dot{x}_i & \cdots & \sum_{i=1}^m\Gamma_{im}^m\dot{x}_i \end{pmatrix}\begin{pmatrix} f_1 \\ \vdots \\ f_m \end{pmatrix} \end{align} と書けるのでベクトル場 の成分
に関して線形の微分方程式となっていることが分かります。したがって、点
における接ベクトル
を任意に与えると、曲線
に沿って平行なベクトル場であって、
を満たすものが、初期条件
のもとでの上の線形微分方程式の解として一意に定まります。このようにして定まる
を曲線
に沿って
を
から
まで平行移動して得られる接ベクトルと言います。
平行移動を定める線形微分方程式の中には接続係数 が含まれていて、この接続係数はアファイン接続から定まります。平行移動は異なる2点の接空間の要素である接ベクトルを関係付けていますから、アファイン接続は異なる2点の接空間のつながり方(関係性)を定めているというように考えることができます。
参考文献
(1) アファイン接続などの説明の参考にしました。
(2) 平行の概念を曲線を使って定義する理由の解説を参考にしました。
(3) 多様体がユークリッド空間の部分多様体である場合には、方向微分の接空間への射影が共変微分になることの説明の参考にしました。

Optimization Algorithms on Matrix Manifolds
- 作者: P. A. Absil,R. Mahony,R. Sepulchre
- 出版社/メーカー: Princeton Univ Pr
- 発売日: 2007/12/03
- メディア: ハードカバー
- この商品を含むブログを見る

