射影行列 - 初級Mathマニアの寝言

この記事では射影行列について解説します。

射影行列の定義と性質

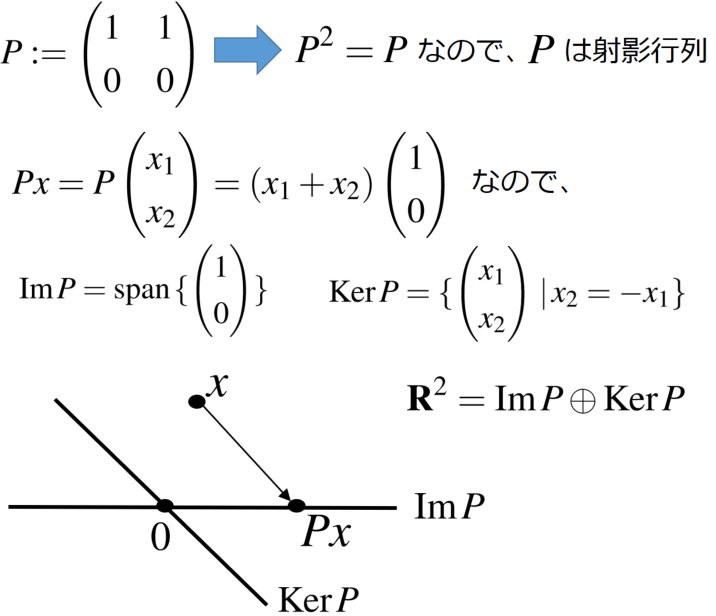
行列 $P:{\bf R}^n\rightarrow {\bf R}^n$ が射影行列であるとは、\begin{align} P^2 =P \end{align} を満たすときに言います。

行列 $P:{\bf R}^n\rightarrow {\bf R}^n$ が射影行列のとき、\begin{align} Q:= I_n-P \end{align} も射影行列であり（ $I_n$ は $n\times n$ の単位行列）、\begin{align} PQ=QP =0 \end{align} であり、\begin{align} {\bf R}^n = {\rm Im}\, P\oplus {\rm Im}\, Q\end{align} が成り立ちます。さらに、\begin{align} {\rm Ker}\, P = {\rm Im}\, Q\end{align} が成り立ち、\begin{align} {\bf R}^n = {\rm Im}\, P\oplus {\rm Ker}\, P\end{align} となります。

ここで、 $\oplus$ は以下の記事で紹介した直和を表しています。

$Q$ が射影行列、 $PQ=QP=0$ は明らかなので、まずは ${\bf R}^n = {\rm Im}\, P\oplus {\rm Im}\, Q$ が成り立つことを示します。任意の $x\in {\bf R}^n$ は $x=I_n x =(P+Q)x=Px+Qx\in {\rm Im}\, P+{\rm Im}\, Q$ となるので ${\bf R}^n={\rm Im}\, P+{\rm Im}\, Q$ が成り立ちますので ${\rm Im}\, P\cap {\rm Im}\, Q=\{0\}$ が成り立つことを確かめたら良いです。そこで、任意の $x\in {\rm Im}\, P\cap {\rm Im}\, Q$ をとってみると、ある $x_1, x_2\in {\bf R}^n$ によって $x = Px_1 = Qx_2$ が成り立ちますので、 $P^2x_1 =PQx_2 = 0$ が成り立つことが分かります。また、 $P^2=P$ なので $Px_1=0$ となり、 $Px_1 = x$ なので $x=0$ が成り立つことになり、 ${\rm Im}\, P\cap {\rm Im}\, Q=\{0\}$ が示せました。次に、 ${\rm Ker}\, P = {\rm Im}\, Q$ が成り立つことを示します。任意の $x\in {\rm Ker}\,P$ をとると、 $Px =0$ なので $x=(I_n-P)x=Qx\in {\rm Im}\,Q$ となり、 ${\rm Ker}\,P\subset {\rm Im}\, Q$ が分かります。また、 $PQ=0$ なので ${\rm Im}\,Q\subset {\rm Ker}\, P$ が成り立つので、 ${\rm Ker}\, P = {\rm Im}\, Q$ が言えました。

上のことは ${\bf R}^n$ 上の射影行列が与えられたら ${\bf R}^n$ の直和分解が得られることを示していますが、逆に ${\bf R}^n$ の直和分解が与えられたら射影行列が定まります。

${\bf R}^n= V_1\oplus V_2$ ならば、 $V_1 = {\rm Im}\, P$ , $V_2= {\rm Im}\, Q$ となる射影行列 $P, Q$ が一意に定まり、 $Q=I_n-P$ となります。言い換えると、 ${\bf R}^n= V_1\oplus V_2$ ならば、任意の $x\in {\bf R}^n$ は $x=x_1+x_2,\,x_1\in V_1,\, x_2\in V_2$ と一意に表されますが、 $x$ を $x_1$ に移す写像 $P$ と $x$ を $x_2$ に移す写像 $Q$ が一意に定まります。この $P$ を $V_2$ に沿った $V_1$ への射影行列、 $Q$ を $V_1$ に沿った $V_2$ への射影行列と言います。

上の $P, Q$ の存在は、 ${\bf R}^n = V_1\oplus V_2$ より、任意の $x\in {\bf R}^n$ はある $x_1\in V_1$ と $x_2\in V_2$ によって $x=x_1+x_2$ と一意に分解できることから $P(x) := x_1 \in V_1$ , $Q(x) := x_2\in V_2$ とおくと、 $P^2=P, Q^2=Q, Q=I_n-P$ が成り立つことから分かります。一意性は、 $x = P_1 x +Q_1x = P_2 x+ Q_2x$ と書いてみると、 $P_1=P_2, Q_1=Q_2$ となることから分かります。

以上のことから次のことが言えます。

行列 $P$ が射影行列であるということは $P$ は ${\rm Ker}\,P$ に沿った ${\rm Im}\,P$ への射影行列であることを意味します。

したがって、射影行列は以下のようにベクトル空間を直和分解する写像のように思えます。

f:id:ogyahogya:20190329101707p:plain

直交射影行列

ユークリッド空間 ${\bf R}^n$ には内積 $(x,y):=x^T y$ が定義されているとします。射影行列 $P:{\bf R}^n\rightarrow {\bf R}^n$ が対称行列、つまり、 $P^T=P$ のとき、 $P$ を直交射影行列と言います。行列 $P$ が直交射影行列だとすると、ユークリッド空間 ${\bf R}^n$ は次のように ${\rm Im}\, P$ と ${\rm Ker}\,P$ に直交直和分解されます。

f:id:ogyahogya:20190329104634p:plain

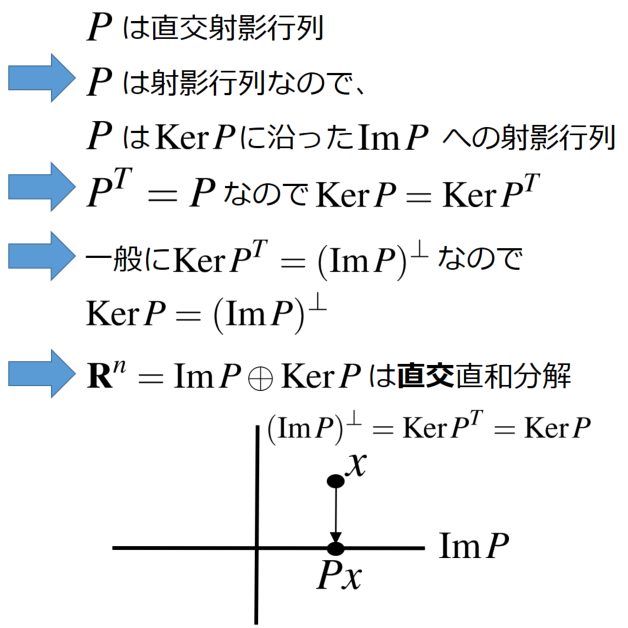
行列 $P$ が直交射影行列ではなく、単なる射影行列だと ${\bf R}^n={\rm Im}\, P\oplus {\rm Ker}\,P$ にはなりますが、これが直交直和とは限らないことが \begin{align} P= \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} \end{align} の上の例から分かります。
一次独立なベクトルたちが張る空間への直交射影行列は次のように表現できます。

f:id:ogyahogya:20190329123501p:plain

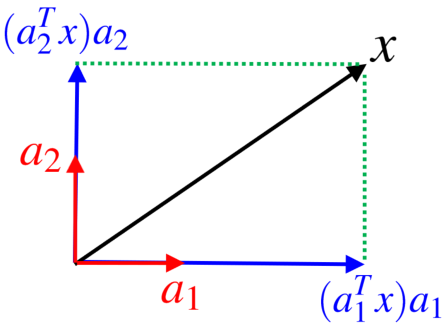
特に、 $a_1,a_2,\ldots,a_m$ が正規直交していると、 ${\rm Im}\, A$ への直交射影行列 $P$ は $A^TA=I$ なので\begin{align} P = AA^T=a_1a_1^T+a_2a_2^T+\cdots +a_ma_m^T \end{align} となり、任意の $x\in {\bf R}^n$ に対して、\begin{align} Px = (a_1^Tx)a_1+(a_2^Tx)a_2+\cdots +(a_m^Tx)a_m \end{align} となります。したがって、 $Px$ は $x$ を各 $a_k$ 軸へ直交射影したベクトルの和として表現されます。例えば、 $x\in {\bf R}^2$ の $Px$ は次のように $a_1$ 軸と $a_2$ 軸へ $x$ を直交射影したベクトルの和ということになります。