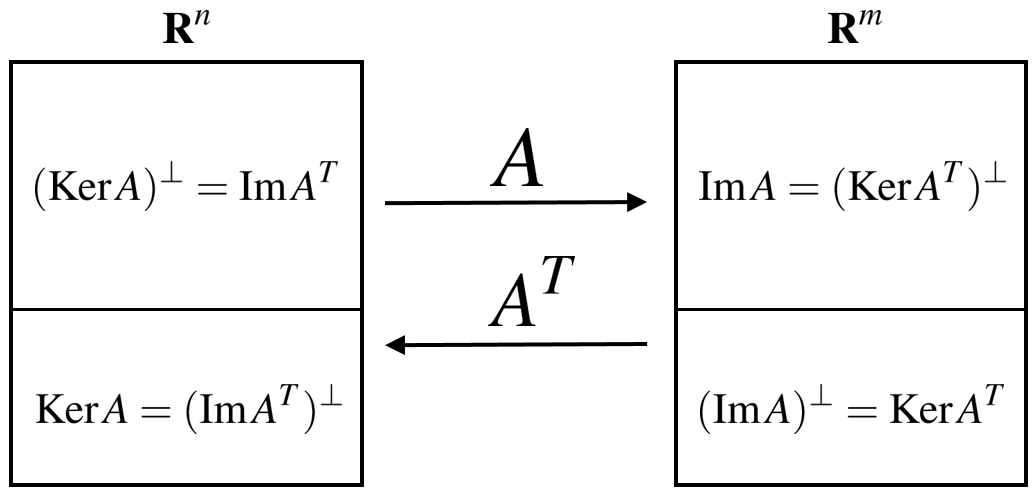
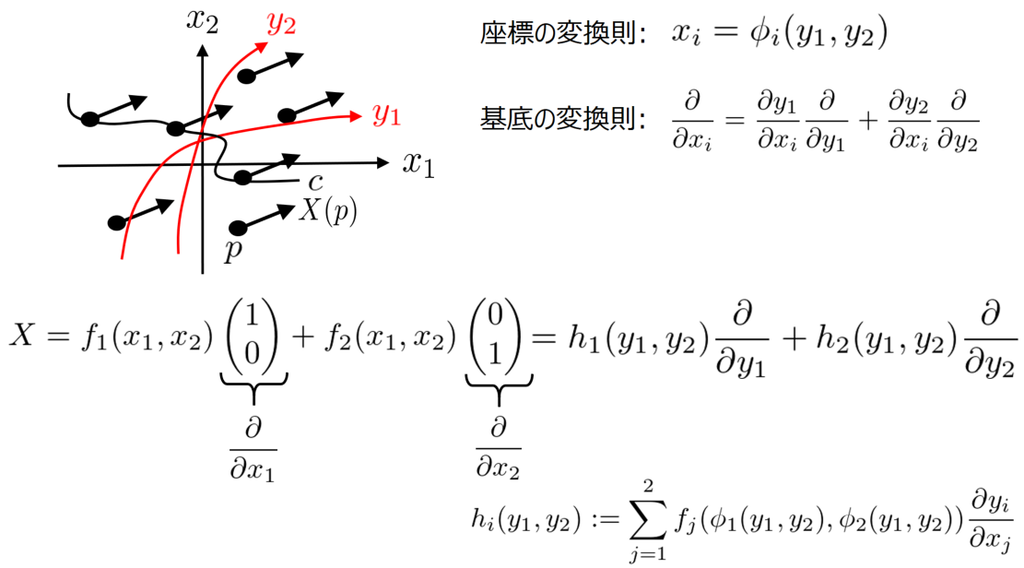
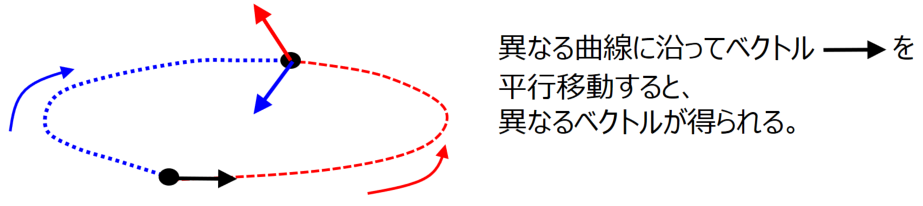
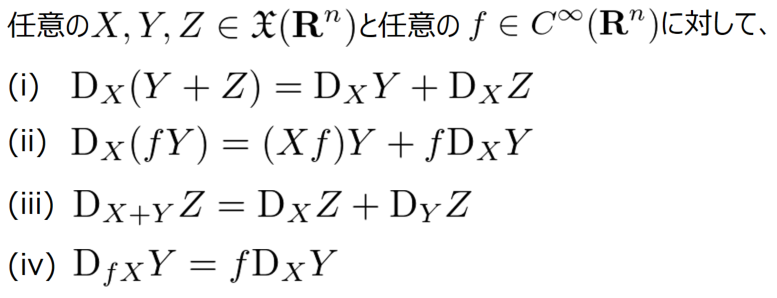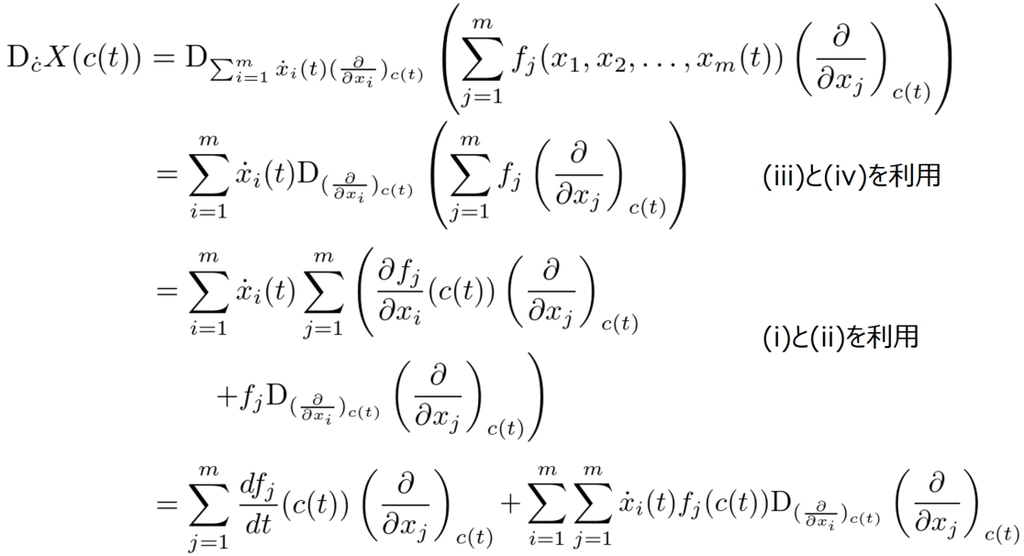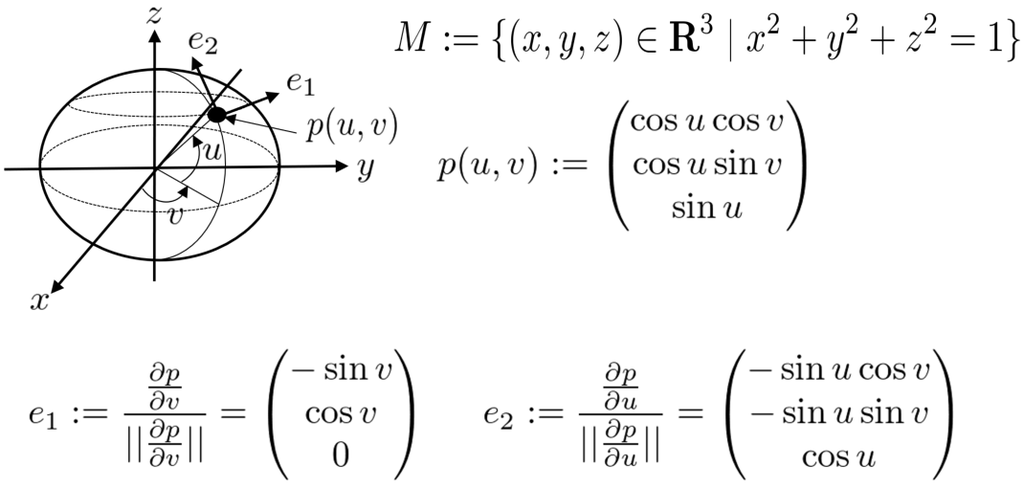この記事では、可制御・可観測な線形システム全体の集合は多様体になることを説明します。ここで言う線形システムとは、
で解説した

のことですが、状態方程式表現は行列の三つ組  で決定するので、一つの線形システムは
で決定するので、一つの線形システムは  の一点である\begin{align} (A,B,C)\end{align}
の一点である\begin{align} (A,B,C)\end{align}
のことだ考えられます。そうすると、線形システム全体の集合とは\begin{align} {\bf R}^{n\times n}\times {\bf R}^{n\times m}\times {\bf R}^{p\times n}\end{align}
のこととなります。この線形システム全体の集合の中には、
で解説した可制御な線形システムや可観測な線形システムが含まれることになり、上の解説記事を注意深く読むと可制御な線形システム全体の集合とは、 \begin{align} S_c:=\{ (A,B,C)\, |\, {\rm rank} \begin{pmatrix} B & AB & \cdots & A^{n-1}B \end{pmatrix}=n\} \end{align}
のことであり、可観測な線形システム全体の集合とは、 \begin{align} S_o:=\{ (A,B,C)\, |\, {\rm rank} \begin{pmatrix} C \\ CA \\ \vdots \\ CA^{n-1} \end{pmatrix}=n\} \end{align}
のことだということになります。つまり、この記事では、
\begin{align} S_c\cap S_o\end{align}
という可制御可観測な線形システム全体の集合が多様体になるということを説明します。多様体については、
を参照してください。
多様体の開集合は多様体になる。
結論から先に言うと、可制御可観測な線形システム全体の集合  が多様体であることは、
が多様体であることは、  が多様体である
が多様体である  の開集合であることから分かります。そこで、多様体の開集合は多様体になるという事実を解説しておきます。あとで、
の開集合であることから分かります。そこで、多様体の開集合は多様体になるという事実を解説しておきます。あとで、  が
が  の開集合だということを説明します。
の開集合だということを説明します。
そもそも開集合とは何かというと、
で説明したように、位相空間の要素のことでした。位相空間  が与えられると、
が与えられると、 の任意の部分集合
の任意の部分集合  に対して、
に対して、
\begin{align} \mathcal{O}_Y:= \{ U\cap Y\,|\, U\in \mathcal{O} \} \end{align}
とすることで、 が
が  の位相になります。このような
の位相になります。このような  を
を  の位相
の位相  から導かれた
から導かれた  の相対位相と呼んで、位相空間
の相対位相と呼んで、位相空間  を
を  の部分空間と呼びます。多様体は上のリーマン多様体の記事で定義したように任意の異なる2点を開集合で分離できるという性質を持ったハウスドルフ空間でした。実は、ハウスドルフ空間
の部分空間と呼びます。多様体は上のリーマン多様体の記事で定義したように任意の異なる2点を開集合で分離できるという性質を持ったハウスドルフ空間でした。実は、ハウスドルフ空間  の部分空間
の部分空間  もハウスドルフ空間になります。なぜなら、任意の
もハウスドルフ空間になります。なぜなら、任意の  ,
,  に対して、
に対して、 はハウスドルフ空間なので、
はハウスドルフ空間なので、 となる
となる  の開集合
の開集合  が存在して、
が存在して、 は
は  の開集合で
の開集合で  となるからです。
となるからです。
上のことから、多様体  の開集合
の開集合  に
に  から導かれた相対位相を導入すると開集合
から導かれた相対位相を導入すると開集合  はハウスドルフ空間となります。さらに、多様体
はハウスドルフ空間となります。さらに、多様体  の
の  級の座標近傍系が
級の座標近傍系が  だとすると、これを
だとすると、これを  に制限した
に制限した  は
は  の
の  級の座標近傍系になります。したがって、多様体
級の座標近傍系になります。したがって、多様体  の任意の開集合は
の任意の開集合は  の位相から導かれた相対位相を導入することで多様体になります。
の位相から導かれた相対位相を導入することで多様体になります。
距離空間は位相空間になる
応用上もっとも重要な空間は距離が定められた空間であり、その距離を使って位相を導入できる、つまり、空間の異なる点たちの近さを議論できるようになります。あとで線形システム全体の集合にも距離を導入して位相空間としますので、ここでは簡単に距離空間について説明しときます。
距離空間の定義は以下の通りです。

ベクトル空間にノルムが導入されたノルム空間は距離空間になります。ここで、ノルム空間の定義は以下の通りです。

実際に、ベクトル空間  にノルム
にノルム  が導入されているとすると、
が導入されているとすると、 上の任意の2点
上の任意の2点  に対して
に対して
\begin{align} d_{\rm norm}(x,y):= ||x-y|| \end{align}
と定めると、 上に距離
上に距離  が導入できます。この
が導入できます。この  をノルム
をノルム  から定められる距離と言います。
から定められる距離と言います。
距離はノルムを使わなくても定義できます。例えば、集合  の任意の2点
の任意の2点  に対して
に対して
\begin{align} d(x,y) := \begin{cases} 1\quad (x\neq y\, のとき) \\ 0 \quad (x=y\, のとき) \end{cases} \end{align}
と定めると、 上に距離
上に距離  が導入できますが、これはあるノルムから定められた距離ではありません。 というのは、ノルムから定められる距離
が導入できますが、これはあるノルムから定められた距離ではありません。 というのは、ノルムから定められる距離  はノルムの定義の(3)から
はノルムの定義の(3)から  を満たしますが、上の距離
を満たしますが、上の距離  はこれを満たさないからです。
はこれを満たさないからです。
距離空間  に対しては次のように距離
に対しては次のように距離  を用いて位相を導入できます。
を用いて位相を導入できます。

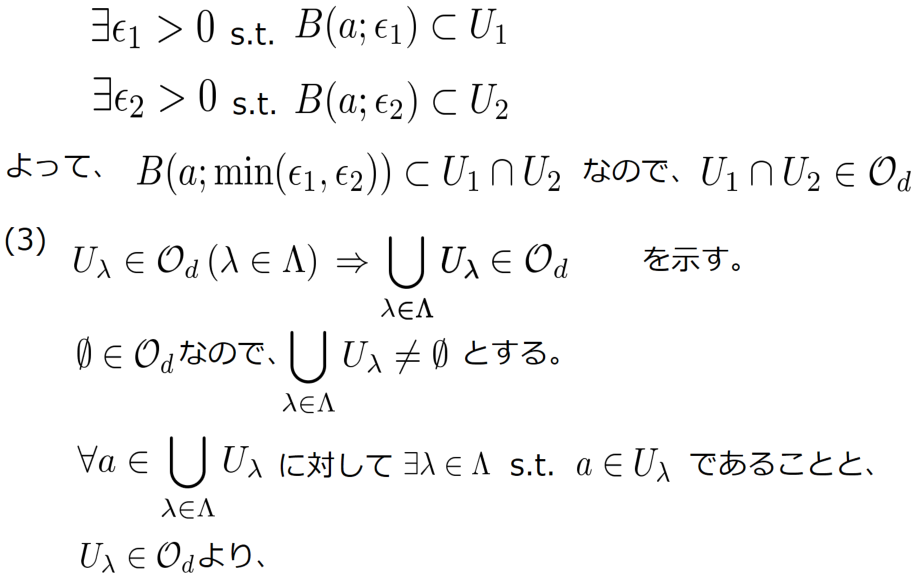
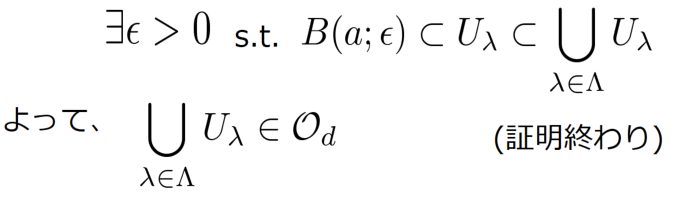
工学系の研究論文は、距離空間を扱うことが多く、位相について何も言わなくても暗黙のうちに上の意味での距離  から定められる位相
から定められる位相  が導入されていることがほとんどです。この記事でも距離空間の位相は上のように距離
が導入されていることがほとんどです。この記事でも距離空間の位相は上のように距離  から定義された位相を導入するとします。
から定義された位相を導入するとします。
線形システム全体の集合  は多様体になる
は多様体になる
線形システム全体の集合  が多様体になることを確認しておきます。
が多様体になることを確認しておきます。
まず、線形システム全体の集合  は次の和(+)とスカラー倍(
は次の和(+)とスカラー倍( )でベクトル空間になります。
)でベクトル空間になります。
\begin{align} (A_1,B_1,C_1)+(A_2,B_2,C_2) &:=(A_1+A_2,B_1+B_2,C_1+C_2) \\ \lambda \cdot (A,B,C)&:= (\lambda A,\lambda B, \lambda C) \end{align}
次に、ベクトル空間である線形システム全体の集合  に以下のノルムを導入します。任意の
に以下のノルムを導入します。任意の  に対して、
に対して、
\begin{align} ||(A,B,C)||:= ||A||_F +||B||_F + ||C||_F \end{align}
この  はフロベニウスノルムと呼ばれており、任意のサイズの行列
はフロベニウスノルムと呼ばれており、任意のサイズの行列  に対して
に対して
\begin{align} ||M||_F:= \sqrt{\sum_{i,j} m_{ij}^2} \end{align}
というように各成分の2乗和の平方根で定義され、行列の集合のノルムとしてよく使われています。上で説明したように、線形システム全体の集合  には
には
\begin{align} d( (A_1,B_1,C_1), (A_2,B_2,C_2) ) &:= ||(A_1,B_1,C_1)- (A_2,B_2,C_2)|| \\ &=||A_1-A_2||_F + ||B_1-B_2||_F+||C_1-C_2||_F\end{align}
というように上のノルムを用いて距離が定義できて距離空間となります。したがって、上で説明したように、この距離  を用いて線形システム全体の集合
を用いて線形システム全体の集合  には位相
には位相  が定義でき位相空間になります。
が定義でき位相空間になります。
この位相空間  がハウスドルフ空間 (任意の異なる2点が開集合で分離できる位相空間) になることは任意の
がハウスドルフ空間 (任意の異なる2点が開集合で分離できる位相空間) になることは任意の  とすると、
とすると、 で
で
\begin{align} B(p_1; d(p_1,p_2)/2)\cap B(p_2; d(p_1,p_2)/2) =\emptyset \end{align}
となることから分かります。さらに、 の座標近傍は
の座標近傍は 自身と行列の3つ組をベクトル化することと同値な微分同相写像
自身と行列の3つ組をベクトル化することと同値な微分同相写像  の組だけの集合
の組だけの集合  であり、これは
であり、これは  級の座標近傍系なので線形システム全体の集合
級の座標近傍系なので線形システム全体の集合  は多様体になります。
は多様体になります。
可制御可観測な線形システム全体の集合  は多様体になる
は多様体になる
可制御可観測な線形システム全体の集合  が多様体になることは
が多様体になることは  と
と  が線形システム全体の集合
が線形システム全体の集合  の開集合であることから従います。なぜなら、
の開集合であることから従います。なぜなら、 と
と  が多様体
が多様体  の開集合なら位相空間の定義から
の開集合なら位相空間の定義から  も開集合となり、多様体の開集合は上で説明したように多様体になるからです。
も開集合となり、多様体の開集合は上で説明したように多様体になるからです。
可制御な線形システム全体の集合  が開集合であることを示します。可観測な線形システム全体の集合
が開集合であることを示します。可観測な線形システム全体の集合  が開集合であることも同様に示せます。
が開集合であることも同様に示せます。 が開集合であるとは、任意の
が開集合であるとは、任意の  とすると、ある
とすると、ある  が存在して、
が存在して、
\begin{align} B( (A,B,C); \delta ) \subset S_c \end{align}
となることを意味しているので、これを示します。 だとすると
だとすると
\begin{align} \begin{pmatrix} B & AB & \cdots & A^{n-1} B \end{pmatrix} \end{align}
の行ベクトル  は1次独立です。つまり、
は1次独立です。つまり、
\begin{align} (\lambda_1, \lambda_2, \ldots, \lambda_n)\neq (0, 0, \ldots, 0)\quad \Rightarrow \quad \lambda_1 v_1+\lambda_2v_2+\cdots +\lambda_n v_n \neq 0 \end{align}
が成り立ちます。行ベクトル  たちは行列
たちは行列  の各成分の和と積から構成されているので、
の各成分の和と積から構成されているので、
\begin{align} f_i: {\bf R}^{n\times n}\times {\bf R}^{n\times m}\times {\bf R}^{p\times n}\rightarrow {\bf R}^{1\times nm}\quad {\rm s.t.}\quad v_i= f_i(A,B,C) \end{align}
となる連続関数  が存在します。連続関数のスカラー倍や連続関数同士の和も連続関数となるので、
が存在します。連続関数のスカラー倍や連続関数同士の和も連続関数となるので、
\begin{align} f(A,B,C):= \lambda_1 f_1(A,B,C) + \lambda_2 f_2(A,B,C)+\cdots +\lambda_n f_n(A,B,C) \end{align}
で定義された関数  も連続関数となります。よって、任意の
も連続関数となります。よって、任意の  に対して、ある
に対して、ある  が存在して、 \begin{align} d( (A,B,C), (A',B',C') ) < \delta \Rightarrow \| f(A,B,C)-f(A',B',C') \|_F < \epsilon \end{align}
が存在して、 \begin{align} d( (A,B,C), (A',B',C') ) < \delta \Rightarrow \| f(A,B,C)-f(A',B',C') \|_F < \epsilon \end{align}
となります。これより、 を適切に選ぶことで
を適切に選ぶことで
\begin{align} \begin{pmatrix} B' & A'B' & \cdots & A'^{n-1} B' \end{pmatrix} \end{align}
の行ベクトルが1次独立にできることを示せれば、ある  が存在して、
が存在して、
\begin{align} B( (A,B,C); \delta ) \subset S_c \end{align}
となることが示せたことになります。いま  が1次独立だったことに注意すると、
が1次独立だったことに注意すると、
\begin{align} \exists \alpha>0\quad {\rm s.t.}\quad ||f(A,B,C)||_F=\alpha \end{align}
が成り立ちます。さらに、\begin{align} | \|f(A',B',C') \|_F - \|f(A,B,C)\|_F | < \| f(A,B,C)-f(A',B',C') \|_F < \epsilon \end{align}
が成り立つので、\begin{align} \| f(A,B,C)\|_F -\epsilon< \| f(A',B',C') \|_F<\| f(A,B,C)\|_F +\epsilon \end{align}
が成り立ちます。よって、\begin{align} \alpha -\epsilon< \| f(A',B',C') \|_F<\alpha +\epsilon \end{align} が成り立つので、 を
を  が成り立つように選ぶと、\begin{align} \| f(A',B',C')\|_F \neq 0 \end{align} が成り立ちます。これは、関数
が成り立つように選ぶと、\begin{align} \| f(A',B',C')\|_F \neq 0 \end{align} が成り立ちます。これは、関数  の作り方から、\begin{align} \begin{pmatrix} B' & A'B' & \cdots & A'^{n-1} B' \end{pmatrix} \end{align} の行ベクトルが1次独立であることを意味しているので、証明完了です。
の作り方から、\begin{align} \begin{pmatrix} B' & A'B' & \cdots & A'^{n-1} B' \end{pmatrix} \end{align} の行ベクトルが1次独立であることを意味しているので、証明完了です。
このように可制御可観測な線形システムの全体の集合  は多様体になって、特に開集合であることが分かりました。
は多様体になって、特に開集合であることが分かりました。  は開集合なので、ある一つの可制御可観測な線形システムの十分小さな近傍内のすべての線形システムは可制御可観測だということになります。実は、可制御可観測な線形システムの全体の集合
は開集合なので、ある一つの可制御可観測な線形システムの十分小さな近傍内のすべての線形システムは可制御可観測だということになります。実は、可制御可観測な線形システムの全体の集合  は線形システム全体の集合
は線形システム全体の集合  の中で稠密であることも示すことができます。つまり、線形システム全体の集合
の中で稠密であることも示すことができます。つまり、線形システム全体の集合  の任意の開集合を
の任意の開集合を  としたとき、
としたとき、 が成り立ちます。このことより、一様にランダムに線形システム
が成り立ちます。このことより、一様にランダムに線形システム  を生成すると、可制御可観測なシステムが得られる可能性が極めて高いということや、可制御可観測でないシステムに微小な摂動が加わっただけで可制御可観測なシステムになるということが言えます。言い換えると、可制御可観測なシステムであっても、実際上はほとんど可制御可観測とは言えないようなシステムもあるということであり、
を生成すると、可制御可観測なシステムが得られる可能性が極めて高いということや、可制御可観測でないシステムに微小な摂動が加わっただけで可制御可観測なシステムになるということが言えます。言い換えると、可制御可観測なシステムであっても、実際上はほとんど可制御可観測とは言えないようなシステムもあるということであり、
で紹介したような指標を使って可制御性や可観測性の大きさを測ることが応用上は重要だということになります。
参考文献
記事を書くにあたって以下の本を参考にしました。
(1) 距離空間とかの部分を参考にしました。
(2) 第2章の定理11の可制御な線形システム全体の集合は開集合であることの証明を参考にしました。
が射影行列であるとは、\begin{align} P^2 =P \end{align} を満たすときに言います。
は以下の記事で紹介した直和を表しています。
が射影行列、
は明らかなので、まずは
が成り立つことを示します。任意の
は
となるので
が成り立ちますので
が成り立つことを確かめたら良いです。そこで、任意の
をとってみると、ある
によって
が成り立ちますので、
が成り立つことが分かります。また、
なので
となり、
なので
が成り立つことになり、
が示せました。次に、
が成り立つことを示します。任意の
をとると、
なので
となり、
が分かります。また、
なので
が成り立つので、
が言えました。
上の射影行列が与えられたら
の直和分解が得られることを示していますが、逆に
の直和分解が与えられたら射影行列が定まります。
には内積
が定義されているとします。射影行列
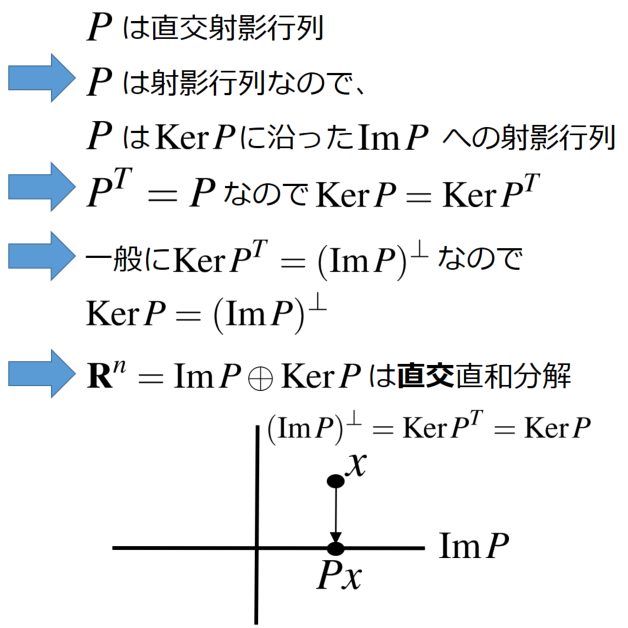
が対称行列、つまり、
のとき、
を直交射影行列と言います。行列
が直交射影行列だとすると、ユークリッド空間
は次のように
と
に直交直和分解されます。
が直交射影行列ではなく、単なる射影行列だと
にはなりますが、これが直交直和とは限らないことが \begin{align} P= \begin{pmatrix} 1 & 1 \\ 0 & 0 \end{pmatrix} \end{align} の上の例から分かります。

が正規直交していると、
への直交射影行列
は
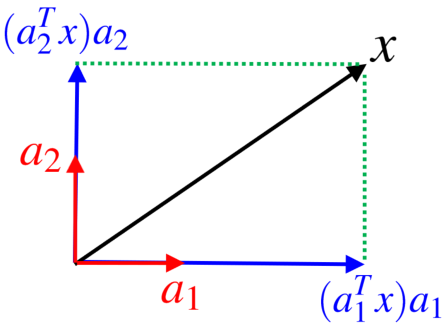
なので\begin{align} P = AA^T=a_1a_1^T+a_2a_2^T+\cdots +a_ma_m^T \end{align} となり、任意の
に対して、\begin{align} Px = (a_1^Tx)a_1+(a_2^Tx)a_2+\cdots +(a_m^Tx)a_m \end{align} となります。したがって、
は
を各
軸へ直交射影したベクトルの和として表現されます。例えば、
の
は次のように
軸と
軸へ
を直交射影したベクトルの和ということになります。
が直交射影行列ならば
となるので以下が成り立つことが分かります。

の直交射影
の大きさは
の大きさ以下になります。行列
が直交射影ではなく、単なる射影行列だとこのようなことは言えません。実際に、次のような例があります。