2018-01-26

グラフラプラシアン

この記事では、電力網のネットワーク、交通網のネットワーク、人間関係のネットワーク、神経ネットワーク、遺伝子ネットワークのようなネットワークシステムの性質を解析する際に重要なグラフラプラシアンについて解説します（枝に向きのないネットワークだけ解説します）。

グラフ、隣接行列、次数行列

下図のように節点と枝から構成されるネットワークを数学的に表現するには、グラフという概念が役立ちます。

グラフとは、節点の集合 $V$ と枝の集合 $E\subset V\times V$ の組 $(V, E)$ のことです。例えば上のネットワークだと節点集合が $\{1, 2, 3, 4, 5, 6\}$ で枝集合が $\{(1,2), (1,3), (1,5), (2,1),(2,3), (3,1), (3,2), (3,6), (4,5), (4,6), (5,1), (5,4), (6,3),(6,4)\}$ です。このように $(i,j)\in E$ なら $(j,i)\in E$ が成り立つグラフを正確には無向グラフといいます（この記事では、無向グラフだけを説明します）。節点は頂点、枝は辺とも呼ばれます。

上のグラフはそれぞれの枝が同等の重要度を持っているとすると、次のような行列で表現できます。

つまり、上のグラフは枝 $(1,2)$ が存在するので行列の $(1,2)$ 成分と $(2,1)$ 成分のところを1として、枝 $(1,4)$ は存在しないので行列の $(1,4)$ 成分と $(4,1)$ 成分を0としています。他の成分も同様に定義すると、上のような対称行列が得られます。逆に上の対称行列から上のグラフが構成できます。もしグラフのそれぞれの枝で重要度が異なる（重み付きグラフという）なら、重要度に応じて1以外の正の実数を行列の成分に定義することで重み付きグラフを対称行列によって表現できます。

より数学的には、グラフ $G=(V,E)$ の枝と重み（重要度）との対応関係を表す関数 $w:E\rightarrow {\bf R}_+$ をグラフ $G$ 上の重み関数といいます( ${\bf R}_+$ は正の実数の集合)。ただし、 $(i,j)\in E$ なら $w ( (i,j) )=w( (j,i) )$ を満たします。この重み付きグラフを $(G,w)$ と書きます。このような重み付きグラフ $(G,w)$ を行列によって表現した対称行列 $A=(a_{ij})$ を隣接行列といい、次のように定義されます。

f:id:ogyahogya:20180123162009p:plain

通常のグラフ $G$ はすべての $(i,j)\in E$ に対して $w( (i,j) )=1$ となる重み付きグラフのことです。

重み付きグラフ $(G,w)$ が与えられたとき、節点 $i\in V$ の次数を $d_i:= \sum_{j=1}^n a_{ij}$ で定義します。ただし、 $n$ はそのグラフの節点の数です。次のように各節点の次数を対角上に並べた対角行列を重み付きグラフ $(G,w)$ の次数行列と呼びます。\begin{align}
D={\rm diag}( d_1, d_2,\ldots, d_n)
\end{align}

例えば上のグラフが与えられたとすると、次数行列は $D={\rm diag} (3, 2, 3, 2, 2, 2)$ です。

グラフラプラシアン、接続行列

重み付きグラフ $(G,w)$ が与えられたとします。このとき、隣接行列 $A$ と次数行列 $D$ を用いて定義される次の行列 $L\in {\bf R}^{n\times n}$ を重み付きグラフ $(G,w)$ のグラフラプラシアンといいます。\begin{align}
L:=D-A
\end{align} グラフラプラシアンの定義からグラフラプラシアン $L\in {\bf R}^{n\times n}$ は固有値 0 を少なくとも一つもち、1をすべての成分に並べたベクトル ${\bf 1}\in {\bf R}^n$ は固有値 0 に対応する固有ベクトルとなります。なぜなら、 $L{\bf 1} = 0$ となるからです。

グラフラプラシアンは接続行列と呼ばれる行列によっても特徴付けられます。接続行列を定義するために、重み付き無向グラフ $(G,w)$ の枝に一意な番号と任意に向きを付けます。例えば、はじめに与えた例のグラフの枝に次のように番号と向きをつけてみましょう。

f:id:ogyahogya:20180124100158p:plain

この枝に番号と向きの付いたグラフは次の行列と対応付けることができます。

つまり、枝が節点から出るときに 1 を、枝が節点に入るときに -1 を、どちらでもないときに 0 を割り当てるというルールで枝に番号と向きの付いたグラフを行列表現できます。このような行列を接続行列といい、正確には次のように定義されます。

重み付き無向グラフの接続行列を定義したとき、各枝には番号が付いています。したがって、枝の上に定義されていた重み関数 $w:E\rightarrow {\bf R}_+$ から各枝に付いている番号の上の関数 $w_e$ が $w_e = w( (i,j) ) = w( (j,i) )$ ( $e= (i,j) = (j,i)$ ) というように定義されます。

重み付き無向グラフ $(G,w)$ のグラフラプラシアン $L\in {\bf R}^{n\times n}$ と接続行列 $B\in {\bf R}^{n\times m}$ は、枝の番号の上に定義された関数 $w_e$ を用いて次の関係で結ばれます。

この等式は枝に任意に向きを付けた接続行列から、グラフラプラシアンという枝の向きに独立な行列を構築できることを意味しています。また、この等式から重み付き無向グラフ $(G,w)$ のグラフラプラシアンは固有値 0 を少なくとも一つ持つ半正定値対称行列であることが即座に分かります。この等式の証明は以下の通りです。

f:id:ogyahogya:20180124164228p:plain

f:id:ogyahogya:20180124164354p:plain

f:id:ogyahogya:20180124164514p:plain

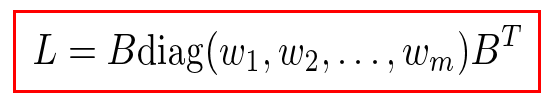
グラフラプラシアンという名前の由来

グラフラプラシアンという名前はベクトル解析で登場するラプラシアンという作用素に由来します。ここでは重みのない無向グラフ $(G,w)$ 、つまり任意の $(i,j)\in E$ に対して $w( (i,j) ) =1$ となる無向グラフのグラフラプラシアンがどのようにラプラシアンに関係しているかを説明します。

まず、グラフラプラシアン $L\in {\bf R}^{n\times n}$ のベクトル $\psi\in {\bf R}^n$ への作用は次のようになることに注意します。

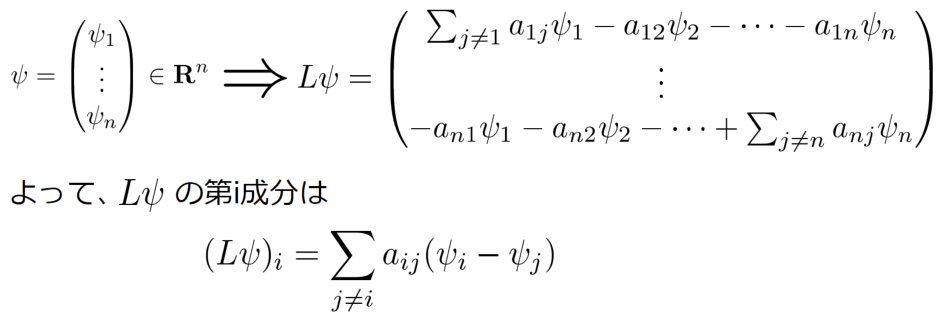
次に、以下のような向きと重みのない格子グラフを考えます。

この格子グラフの節点を格子座標 $(x,y)$ で表し、節点の集合を $V$ とすると、上図のようにグラフの境界から離れた節点の次数は4なので、グラフラプラシアン $L$ の節点集合上の関数 $\phi: V\rightarrow {\bf R}$ への作用は、グラフラプラシアンのベクトルへの作用のアナロジーで、\begin{align}
(L\phi)(x,y) = 4\phi (x,y) -\phi(x+1,y) -\phi(x-1,y)-\phi(x,y+1)-\phi(x,y-1)
\end{align}となると考えられます。

さらに今度は同じ記号を使ってユークリッド空間 ${\bf R}^2$ 上のテイラー展開可能な関数 $\phi: {\bf R}^2\rightarrow {\bf R}$ を考えます。このとき、 $h$ を非常に小さいとして、 $\phi(x+h,y)$ と $\phi(x,y+h)$ を点 $(x,y)\in {\bf R}^2$ の周りでテイラー展開すると、\begin{align}
\phi(x+h,y) &= \phi(x,y) + h\frac{\partial \phi}{\partial x}(x,y) + \frac{h^2}{2!}\frac{\partial^2 \phi}{\partial x^2}(x,y)+\cdots \\ \phi(x,y+h) &= \phi(x,y) + h\frac{\partial \phi}{\partial y}(x,y) + \frac{h^2}{2!}\frac{\partial^2 \phi}{\partial y^2}(x,y)+\cdots
\end{align}となるので、\begin{align}
\frac{\partial^2 \phi}{\partial x^2}(x,y) &\approx \frac{\phi(x+h,y)+\phi(x-h,y)-2\phi(x,y)}{h^2} \\ \frac{\partial^2 \phi}{\partial y^2}(x,y) &\approx \frac{\phi(x,y+h)+\phi(x,y-h)-2\phi(x,y)}{h^2}
\end{align}となります。よって、\begin{align}
\frac{\partial^2 \phi}{\partial x^2}(x,y)+ \frac{\partial^2 \phi}{\partial y^2}(x,y) \approx \frac{\phi(x+h,y)+\phi(x-h,y)+\phi(x,y+h)+\phi(x,y-h)-4\phi(x,y)}{h^2}
\end{align}となりますが、 ${\bf R}^2$ 上のラプラシアン $\Delta$ は $\Delta= \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ なので、\begin{align}
(\Delta \phi)(x,y) \approx \frac{\phi(x+h,y)+\phi(x-h,y)+\phi(x,y+h)+\phi(x,y-h)-4\phi(x,y)}{h^2}
\end{align}となります。したがって、グラフラプラシアン $L$ はラプラシアン $\Delta$ の(-1)倍の離散化とみなせます。

グラフラプラシアンの名前の由来のもう少し深いところ

上で説明したように、グラフ理論のグラフラプラシアンとベクトル解析のラプラシアンには密接な関係があります。ここでは先ほどと同様に重みのない無向グラフを対象として、もう少し深いつながりを見たいと思います。

ベクトル解析のラプラシアン $\Delta$ は\begin{align} \Delta = {\rm div} ({\rm grad}) \end{align}のことです。ここで、 ${\rm grad}$ は勾配(gradient)の作用素、 ${\rm div}$ は発散(divergence)の作用素を表します。つまり、ラプラシアンは勾配と発散の合成によって表現されます。

このことと同様なことがグラフラプラシアンでも言えて、接続行列の転置が勾配に対応し、接続行列が発散に対応します。つまり、\begin{align} L = BB^T \end{align} が成り立ちます。この関係式は上で既に証明しています（今は重みなしで考えているので $w_1=w_2=\cdots =w_m=1$ であることに注意）。つまり、上で証明したグラフラプラシアンと接続行列の関係式は、ベクトル解析のラプラシアンが勾配と発散によって関係づけられていることから自然な関係式なのだということが分かります。

まず、接続行列の転置 $B^T\in {\bf R}^{m\times n}$ が勾配 ${\rm grad}$ に対応することを示します。 $B^T$ を $\phi = (\phi_1,\phi_2,\ldots, \phi_n)\in {\bf R}^n$ に作用させると、第k成分は\begin{align} (B^T\phi)_k = \sum_{i=1}^n B_{ik} \psi_i \end{align} となります。接続行列 $B$ の行は節点、列は枝に対応していたので、 $k=(i,j)\in E$ で節点iから節点jに行く向きが付いてると $B$ の第k列の第i成分は1、第j成分は-1になります。よって、\begin{align} (B^T\phi)_k = \phi_i-\phi_j \end{align}となり、節点集合上に定義された関数の差、つまり、勾配として $(B^T\phi)_k$ を見ることができます。さらに、 $B^T\phi$ 自身は枝上に定義された関数として解釈できます。したがって、ベクトル解析の勾配はスカラー場（関数）をベクトル場（関数）にしましたが、グラフ上の勾配（接続行列の転置）は節点集合上の関数を枝集合上の関数にすると解釈できます。

次に、接続行列 $B\in {\bf R}^{n\times m}$ が発散 ${\rm div}$ に対応することを示します。 $\psi = (\psi_1,\psi_2,\ldots, \psi_m)\in {\bf R}^m$ として $B$ を作用させると、\begin{align} (B\psi)_i = \sum_{k=1}^m B_{ik}\psi_k \end{align} となりますが、接続行列の定義から、これは\begin{align} (B\psi)_i = \sum_{節点iから出る枝k} \psi_k -\sum_{節点iに入る枝k}\psi_k \end{align}を意味しています。例えば、以下のような感じです。

これは、ベクトル解析の発散のイメージそのものです。ベクトル解析の発散のイメージについては、

ＥＭＡＮの物理学・電磁気学・ガウスの定理の証明

あたりを参考にしてください。

以上をまとめると、以下の対応関係が得られます。

f:id:ogyahogya:20180125165128p:plain

先ほどまで、勾配、発散、ラプラシアンはユークリッド空間上の関数に作用させていましたが、リーマン多様体上の関数に対しても勾配、発散、ラプラシアンが定義でき、上のような対応関係が得られます。リーマン多様体については、以下を参考にしてください。

ogyahogya.hatenablog.co

参考文献

記事を書くにあたって参考にした文献です。

(1) 重み付きグラフとグラフラプラシアンの定義のところを参考にしました。グラフ理論の初歩的な内容の解説と、初歩的なグラフ理論の制御工学の問題への応用が分かりやすく説明してあります。

マルチエージェントシステムの制御 (システム制御工学シリーズ)

作者: 東　俊一,永原　正章,石井　秀明,林　直樹,桜間　一徳,畑中　健志
出版社/メーカー: コロナ社
発売日: 2015/08/28
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

(2) ベクトル解析の勾配、発散、ラプラシアンがグラフ理論の接続行列の転置、接続行列、グラフラプラシアンにそれぞれ対応しているという解説を参考にしました。この本は電気回路のネットワークの性質をグラフ理論の概念を使って色々解析しています。面白いです。

線形代数とネットワーク

作者: ??金久
出版社/メーカー: 日本評論社
発売日: 2017/03/08
メディア: 単行本
この商品を含むブログを見る

(3) リーマン多様体上の関数への勾配、発散、ラプラシアンの作用素が詳しく説明されています。

ラプラシアンの幾何と有限要素法 (朝倉数学大系)

作者: 浦川肇
出版社/メーカー: 朝倉書店
発売日: 2009/10/01
メディア: 単行本
クリック: 5回
この商品を含むブログを見る

2017-11-09

最小平均二乗誤差推定値は条件付き期待値

確率とか

この記事では、下図のように $y$ を観測してパラメータ $x$ を推定しようとしたとき、推定したいパラメータ $x$ と推定値 $\hat{x}$ の二乗誤差 $||x-\hat{x}||^2$ の期待値が最小となる推定値（最小平均二乗誤差推定値） $\hat{x}$ は条件付き期待値 $E(x|y)$ で与えられ、この推定値は不偏推定値になることを説明します。 f:id:ogyahogya:20171108130548p:plain

ここでは、 $x\in {\bf R}^n$ , $y\in {\bf R}^p$ , $\hat{x}\in {\bf R}^n$ として、 $||\cdot||$ をユークリッドノルムとします。

推定したいパラメータ $x$ と観測値 $y$ は確率変数だと考える。そうすると、推定値 $\hat{x}$ も確率変数だと考えるのが自然になる。

この記事の中では、推定したいパラメータ $x$ と観測値 $y$ は確率変数だと考えます。そのとき、推定値 $\hat{x}$ も確率変数だと考えるのが自然になります。これらの理由を以下で説明します。

推定したいパラメータ $x$ は全知全能の神様にとっては確定値かもしれませんが、「 $x$ は $\hat{x}$ か？」と思っている人にとっては確定値ではなく、確率的にしか決められないものかもしれません。推定したいパラメータ $x$ は確率的に定まるものだと考えることは、数学的には、 $x$ は確率変数だと考えることに相当します。確率変数は下の記事で紹介しています。

ogyahogya.hatenablog.com

推定したいパラメータ $x$ が確率変数だと考えると、観測値 $y$ も確率変数だと考えることが自然なことが多いです。実際に、観測値は $y=x+v$ というように、確率変数である $x$ に確率変数である雑音 $v$ が加算されたものかもしれず、もしそうなら観測値 $y$ は確率変数となるためです。他にも $y$ が $x$ の関数として表現される多くの場合に、 $y$ は確率変数ということになります。

推定値 $\hat{x}$ は観測値 $y$ の関数だと考えて、関数 $f$ を用いて $\hat{x} = f(y)$ という関係があると考えるのが自然です。なぜなら、推定値 $\hat{x}$ は観測値 $y$ を参考にして決定するはずだからです。したがって、観測値 $y$ が確率変数なら $\hat{x}$ も確率変数だと考えることができます(関数 $f$ が可測関数という連続関数を含む応用上とても広いクラスの関数なら、 $y$ が確率変数のときに $f(y)$ も確率変数となる)。

なぜ $E(||x-\hat{x}||^2)$ を最小化するのか

この記事の冒頭で、二乗誤差 $||x-\hat{x}||^2$ の「期待値」を最小にする $\hat{x}$ は条件付き期待値 $E(x|y)$ だということを紹介すると書きましたが、なぜ二乗誤差 $||x-\hat{x}||^2$ そのものではなく、その「期待値」を最小にする $\hat{x}$ を考えるのでしょうか？その理由は、二乗誤差 $||x-\hat{x}||^2$ は $\hat{x}=x$ のときに最小値0となりますが、ここでは $x$ を確率変数だと考えるため $\hat{x}=x$ とすることができない上に、 $x$ が不明なので、どうやって $||x-\hat{x}||^2$ を小さくできるかも分からないためです。そのため、代わりに二乗誤差の期待値 $E(||x-\hat{x}||^2)$ の最小化を考えるのです。

$E(||x-\hat{x}||^2)$ を最小化するとは、もっと正確にはどういうことなのか

二乗誤差の期待値 $E(||x-\hat{x}||^2)$ は関係式 $\hat{x}=f(y)$ の関数 $f$ が与えられたら、次のように計算できます。

\begin{align*} E(||x-\hat{x}||^2) &= E(||x-f(y)||^2) \\ &= \int_{ {\bf R}^p } \int_{ {\bf R}^n} ||x-f(y)||^2 p(x,y) dx dy \end{align*}

この式を見れば分かるように、二乗誤差の期待値 $E(||x-\hat{x}||^2)$ は同時確率分布 $p(x,y)$ が与えられたら関数 $f$ の関数なので、 $E(||x-\hat{x}||^2)$ を

\begin{align*} R(f) := E(||x-\hat{x}||^2) \end{align*}

と書けます。このように、二乗誤差の期待値 $E(||x-\hat{x}||^2)$ を最小化するということは、同時確率分布 $p(x,y)$ が任意に与えられたときに関数 $R(f)$ を最小化する関数 $f$ を求めることを意味しています。

※関数 $R$ は関数 $f$ の関数だということから、汎関数(関数の関数)だということになります。

汎関数 $R(f)$ を最小にする関数 $f(y)$ は条件付き期待値 $E(x|y)$ になる

二乗誤差の期待値 $E(||x-\hat{x}||^2)$ 、つまり汎関数 $R(f)$ の最小化を考えてみましょう。まず、 $R(f)$ は

\begin{align*} R(f) &= \int_{ {\bf R}^p } \int_{ {\bf R}^n} ||x-f(y)||^2 p(x,y) dx dy \\ &=\int_{ {\bf R}^p } R_c(f) p(y) dy \end{align*}

となることに注意します。ここで、

\begin{align*} R_c(f):= \int_{ {\bf R}^n} ||x-f(y)||^2 p(x|y) dx =E(||x-f(y)||^2 | y) \end{align*}

です。

実は、 $R(f)$ を最小にする $f$ と $R_c(f)$ を最小にする $f$ は一致します。したがって、 $R(f)$ を最小化する $f$ の代わりに、 $R_c(f)$ を最小化する $f$ を求めれば良いということになります。

実際に、 $R_c(f)$ を計算してみると以下のようになります。\begin{align*} R_c(f) &= E(||x-f(y)||^2 | y) \\ &= E(|| (x-E(x|y)) + (E(x|y)-f(y))||^2 | y) \\ &= E(||x-E(x|y)||^2 | y) + ||E(x|y)-f(y)||^2 \\ &\geq E(||x-E(x|y)||^2 | y) \end{align*}

最後の不等式で等号が成り立つのは $f(y) = E(x|y)$ のときなので、 $R_c(f)$ を最小にする関数 $f(y)$ は条件付き期待値 $E(x|y):= \int_{{\bf R}^n} x p(x|y) dx$ だということが分かります。よって、最小平均二乗誤差推定値は $\hat{x} = E(x|y)$ となります。

※上の証明の中で突然 $E(x|y)$ が出てきました。これは、最小平均二乗誤差推定値は $\hat{x} = E(x|y)$ となることを知っていないと思いつかないかもしれません。このことを知らないとして、関数 $R_c$ を最小にする関数 $f$ を求めるためには微分 $\frac{\partial R_c}{\partial f}=0$ を満たす $f$ を求めれば良さそうです。実際に、このへんの話はカルマンフィルタ関係の本によく載っているのですが、多くの本のなかで微分 $\frac{\partial R_c}{\partial f}=0$ を満たす $f$ を求めています。が、実はこの微分といっているものは通常の微分だと考えることができません。なぜなら $f$ は数値ではなく関数だからです。ということで、微分 $\frac{\partial R_c}{\partial f}$ を計算するといっても通常の意味の微分は計算できません。では、どうするかというと汎関数 $R_c$ の変分(汎関数微分)を計算し、その変分がゼロになる関数 $f$ が答えだということになります。つまり、力学でオイラー・ラグランジュ方程式を導出する際にラグランジアンの作用積分の変分を計算したように、汎関数 $R_c$ の変分を計算すれば良いということになります。では実際に汎関数 $R_c$ の変分を計算してみましょう。汎関数 $R_c$ の点 $f$ における $h$ 方向への微分は

\begin{align*} \delta R_c(f)[h] := \lim_{\epsilon\rightarrow 0} \frac{R_c (f+\epsilon h) -R_c(f)}{\epsilon} \end{align*} となります（上記の $\delta R_c(f)$ がゼロとなる関数 $f$ を見つけることを変分問題 $\delta R_c(f)=0$ と書く）。汎関数 $R_c(f)$ の定義から、

\begin{align*} R_c(f+\epsilon h) -R_c(f) = \int_{{\bf R}^n} \left( 2\epsilon (x-f(y))^T h(y) + \epsilon^2 ||h(y)||^2 \right) p(x|y) dx \end{align*}

となります。よって、

\begin{align*} \delta R_c(f)[h] &= 2 \int_{ {\bf R}^n} (x-f(y))^T h(y) p(x|y) dx \\ &= 2(E(x|y)-f(y))^T h(y) \end{align*}

ということになります。したがって、 $f(y)=E(x|y)$ のとき $\delta R_c(f)=0$ となることが分かりました。

最小平均二乗誤差推定値 $\hat{x} = E(x|y)$ は不偏推定値

一般に、推定したいパラメータ $x$ と推定値 $\hat{x}$ の誤差の期待値 $E(x-\hat{x})$ がゼロになるとき推定値 $\hat{x}$ は推定したいパラメータ $x$ の不偏推定値だと言います。つまり、推定したいパラメータの期待値と推定値の期待値が一致しているときに、その推定値は不偏だと言うのです。

最小平均二乗誤差推定値 $\hat{x}=E(x|y)$ は次のように不偏推定値だということが分かります。

\begin{align*} E(\hat{x}) &= E( E(x|y)) \\ &= \int_{{\bf R}^p} \left( \int_{{\bf R}^n} x p(x|y) dx \right) p(y) dy \\ &= \int_{{\bf R}^p} \int_{{\bf R}^n} x p(x,y) dx dy \\ &= \int_{ {\bf R}^n} x \int_{ {\bf R}^p} p(x,y) dy dx\\ &= \int_{{\bf R}^n} x p(x) dx = E(x) \end{align*}

参考文献

記事を書くにあたって参考にした文献です。

(1) 理論的なことがしっかり書いてる。

応用カルマンフィルタ

作者: 片山徹
出版社/メーカー: 朝倉書店
発売日: 2000/02/01
メディア: 単行本
クリック: 6回
この商品を含むブログを見る

この記事の中では、二乗誤差 $||x-\hat{x}||^2$ の期待値の最小化を考えましたが、この本の中では、他にも絶対誤差の期待値や一様誤差の期待値の最小化も考えられており、条件付き確率分布 $p(x|y)$ がガウス分布に従うなら、絶対誤差と一様誤差の期待値の最小値を与える関数は二乗誤差の期待値の最小値を与える条件付き期待値 $E(x|y)$ に一致することが説明されています。ということで、条件付き期待値 $E(x|y)$ は他の評価指標を使っても最も良い推定値になることがあるということが分かります。

ガウス分布は、以下の記事で説明したように中心極限定理と密接に関連した確率分布で応用上よくでてきます。

ogyahogya.hatenablog.com(2) 上の参考文献と同じ著者の本。汎関数の変分を計算すべきところを普通の微分のように計算しているのは誤りであることに注意。この本のように英語の本でも普通の微分のように計算しているものが多々あります。。。

非線形カルマンフィルタ

作者: 片山　徹
出版社/メーカー: 朝倉書店
発売日: 2011/11/30
メディア: 単行本（ソフトカバー）
この商品を含むブログ (1件) を見る

2017-07-04

可制御性グラミアンと可観測性グラミアン

制御理論

対象とする線形システム

f:id:ogyahogya:20170630161131p:plain

の可制御性と可観測性の定義は

ogyahogya.hatenablog.com

で紹介しましたが、この記事では可制御性と可観測性の「大きさ」を定量的に測る手段を紹介します。線形システムについては

ogyahogya.hatenablog.com

で紹介しています。この記事の中では行列 $A$ を安定、つまり、 $A$ のすべての固有値の実部は負であると仮定します。

入力エネルギー最小化問題

まず、線形写像 $\Psi_c: L^2(-\infty,0] \rightarrow {\bf R}^n$ を

f:id:ogyahogya:20170630161918p:plain

と定義します。ここで、 $L^2(-\infty,0]$ は区間 $(-\infty,0]$ 上で定義された2乗可積分な関数全体の線形空間です。このような空間については、

ogyahogya.hatenablog.com

でも紹介しています。この $\Psi_c(u)$ は無限の過去 $t=-\infty$ に状態が0であるときの現在 $t=0$ の状態 $x(0)$ を表していると解釈できます。実際に、 $\lim_{t\rightarrow -\infty} x(t) =0$ とすると、行列 $A$ が安定なので、\begin{align}
x(0) &= \lim_{t_0\rightarrow -\infty}\left(e^{-At_0}x(t_0)\right) + \int_{-\infty}^0 e^{A(0-t)}Bu(t)dt\\&=\int_{-\infty}^0 e^{-At}Bu(t)dt = \Psi_c(u)
\end{align}となるからです。

$v_1, v_2\in L^2(-\infty,0]$ とするとき、 $\langle v_1, v_2 \rangle_2:= \int_{-\infty}^0 v_1^T(t) v_2(t) dt$ によって $\langle \cdot, \cdot \rangle_2$ を定義し、 $||v_1||_2:=\sqrt{\langle v_1, v_1 \rangle_2}$ によって $||\cdot ||_2$ を定義します。

このとき、次の入力エネルギー最小化問題を考えます。

f:id:ogyahogya:20170630164230p:plain

ただし、 $||\cdot||$ はユークリッドノルムを表します。この問題は、「状態を原点から単位球面上に到達させることが可能な2乗可積分な入力の中で、エネルギーが最小になるものを求めよ。」ということを意味しています。

可制御性グラミアン

上の入力エネルギー最小化問題と次の可制御性グラミアン

f:id:ogyahogya:20170703161119p:plain

は密接な関係があります。ここでは、その関係を見るための準備をします。

線形作用素 $\Psi_c$ と行列 $W_c$ の間には次の関係が成り立ちます。

f:id:ogyahogya:20170703161504p:plain

ここで、 $\Psi_c^*$ は $\Psi_c$ の共役作用素です。共役作用素はこちらで説明しましたので、興味がありましたら参照してください。

ogyahogya.hatenablog.com

上の関係が成り立つことは次のように確認できます。

f:id:ogyahogya:20170703163148p:plain

f:id:ogyahogya:20170703163648p:plain

任意の $\xi\in {\bf R}^n$ に対して、上記の式が成り立つことから $W_c=\Psi_c\Psi_c^*$ が成り立つことが証明できました。

可制御性グラミアンの表式から $W_c$ は半正定値対称行列だということが分かります。実は、線形システムが可制御であることと、 $W_c$ が正定値対称行列であることは等価です。ここでは簡単のために、線形システムは可制御であるとして話を進めます。

直交射影

入力エネルギー最小化問題の解と可制御性グラミアンの関係を、すっきりと理解するために、直交射影の概念を紹介します。

f:id:ogyahogya:20170704093559p:plain

直交射影には、次の性質があります。

f:id:ogyahogya:20170704100020p:plain

入力エネルギー最小化問題の解と可制御性グラミアンの関係

入力エネルギー最小化問題の解は、次のように可制御性グラミアン $W_c$ を用いて表現できることが分かります。

f:id:ogyahogya:20170703164814p:plain

実は、ある直交射影 $P: L^2(-\infty,0] \rightarrow L^2(-\infty,0]$ が存在し、(※)を満たす任意の $u\in L^2(\infty,0]$ に対して、 $Pu=u_{最適}$ となって $Pu$ も(※)を満たすことが示せます。直交射影の定義の下で示したように、 $||Pu||_2 \leq ||u||_2$ なので、上の主張が成り立つということになります。

そのような直交射影 $P$ は

f:id:ogyahogya:20170704101524p:plain

で与えられます。 $Pu$ が(※)を満たすことは、

f:id:ogyahogya:20170704101724p:plain

から分かります。さらに、★が直交射影であることも少し計算すれば示せます。

さらに、入力エネルギーと可制御性グラミアンの間には、次の関係が成り立つことが分かります。

f:id:ogyahogya:20170704102951p:plain

なお、 $W_c$ の逆行列 $W_c^{-1}$ は、線形システムを可制御であると考えているので存在します。

可制御性グラミアンの幾何学的解釈

ここでは、入力 $u\in L^2(-\infty,0]$ ( $||u||_2\leq 1$ ) で到達可能な状態を可制御性グラミアン $W_c$ を用いて特徴付けます。この特徴付けは次の事実に基づきます。

f:id:ogyahogya:20170704111337p:plain

f:id:ogyahogya:20170704111350p:plain

上で示したことから、入力 $u\in L^2(-\infty,0]$ ( $||u||_2\leq 1$ ) で到達可能な状態は $W_c^{1/2} x$ ( $||x||\leq 1$ )だということが分かりました。

以上のことから「可制御性の大きさ」、すなわち、「制御のしやすさ」と可制御性グラミアン $W_c$ の関係を調べることができます。このことを見るために、単位エネルギー $||u||_2= 1$ の入力 $u\in L^2(-\infty,0]$ で到達可能な状態の集合は

f:id:ogyahogya:20170704122935p:plain

であることに注意しましょう。今、 $W_c^{1/2}$ の固有値を $\lambda_1,\lambda_2,\ldots, \lambda_n$ 、対応する正規直交固有ベクトルを $v_1,v_2,\ldots,v_n$ とすると、

f:id:ogyahogya:20170704123212p:plain

となり、 $\mathcal{E}_c$ は固有ベクトル $v_1,v_2,\ldots,v_n$ の方向を主軸として固有値 $\lambda_1,\lambda_2,\ldots,\lambda_n$ を主値とする楕円であることが分かります。イメージ図は下のような感じです。

f:id:ogyahogya:20170704123700p:plain

つまり、単位エネルギー $||u||_2= 1$ の入力 $u\in L^2(-\infty,0]$ で原点から最も遠くまで到達可能な方向が可制御性グラミアン $W_c$ の最大固有値に対応する固有ベクトルの方向で、2番目に遠くまで到達可能な方向が２番目に大きい固有値に対応する固有ベクトルの方向、３番目に・・・ということになります。言い換えると、最も制御しやすい方向が可制御性グラミアン $W_c$ の最大固有値に対応する固有ベクトルの方向で、最も制御しにくい方向が $W_c$ の最小固有値に対応する固有ベクトルの方向だということです。

以上から、線系システムが可制御であっても、制御のしやすい方向としにくい方向があり、それらを定量的に調べるためには可制御性グラミアン $W_c$ の固有値と固有ベクトルを調べれば良いということが分かりました。

可観測性グラミアン

次に、観測のしやすさを定量的に評価する可観測性グラミアンについて説明します。

今、現在の状態 $x(0)$ を $x_0$ とします。このとき、 $\Psi_o:{\bf R}^n\rightarrow [0,\infty)$ を

f:id:ogyahogya:20170704142459p:plain

で定義します。線形写像 $\Psi_o$ は $[0,t]$ 上で入力を $u=0$ としたときの線形システムの出力値と関係付きます。なぜなら、 $y(t) = C\exp (At) x_0 = \Psi_o x_0$ が成り立つからです。可制御性グラミアンの時と同様の計算で、 $\Psi_o$ は可観測性グラミアン

f:id:ogyahogya:20170704142729p:plain

と

f:id:ogyahogya:20170704142927p:plain

の関係があることが分かります。ここでは、 $L^2 [0,\infty)$ 上に内積を $\langle f_1, f_2 \rangle_2 := \int_0^{\infty} f_1(t)^Tf_2(t) dt$ で定め、ノルムを $||f||_2:= \sqrt{\langle f, f \rangle_2}$ で定めることにします。すると、出力は $y=\Psi_o x_0$ のため、出力エネルギーが

f:id:ogyahogya:20170704143554p:plain

と可観測性グラミアン $W_0$ を用いて表せることが分かります。可制御性グラミアンの時と同様に、可観測性グラミアン $W_o$ を用いて定義された集合

f:id:ogyahogya:20170704143756p:plain

は楕円であり、主軸は $W_o$ の固有ベクトルの方向で、主値は固有値の平方根ということになります。これは球面上の状態 $x_0$ にも「観測のしやすさ」があり、可観測性グラミアン $W_o$ の最大固有値に対応する固有ベクトルの方向の状態が最も観測しやすく、最小固有値に対応する固有ベクトルの方向の状態が最も観測しにくいという意味になります。（ここで、観測のしやすさを出力エネルギー $||y||_2^2$ の大小で解釈しています。）

参考文献

記事を書くにあたって次の本を参考にしました。

A Course in Robust Control Theory: A Convex Approach (Texts in Applied Mathematics)

作者: Geir E. Dullerud,Fernando Paganini
出版社/メーカー: Springer
発売日: 2000/02/02
メディア: ハードカバー
この商品を含むブログを見る

2017-02-06

行列の指数関数と対数関数

多様体とか

この記事では、行列の指数関数と対数関数について解説します。Lie群とLie環という概念を理解するための準備に相当します。

●行列の内積とノルム

${\bf R}^{n\times n}$ をn行n列の実数を成分に持つ行列全体の集合とします。このとき、 ${\bf R}^{n\times n}$ に以下の内積とノルムを導入できます。

f:id:ogyahogya:20170202134934p:plain

任意の $A, B\in {\bf R}^{n\times n}$ に対して $||AB||\leq ||A||\cdot ||B||$ が成り立つことがコーシー・シュワルツの不等式を使うことで確認できます。

●行列の指数関数

実数 $x$ の指数関数 $e^x$ を $x=0$ の周りでテイラー展開すると $e^x = \sum_{k=0}^{\infty} \frac{1}{k!} x^k$ でした。これと形式的に同じになるように行列の指数関数が次のように定義されます。

f:id:ogyahogya:20170202140703p:plain

右辺の無限級数が収束することは以下のように分かります。

f:id:ogyahogya:20170202140816p:plain

●行列の指数関数の性質

行列の指数関数の性質は以下の結果を利用して明らかにすることができます。

f:id:ogyahogya:20170202144600p:plain

解であることは $\gamma(t)=\exp(tX)$ を左辺と右辺に代入して等しくなることを見れば良いです。一意性は、微分方程式の解の一意性定理から従います。

指数関数の性質を明らかにする前に、二つの行列が可換であるか否かを判定するカッコ積を導入しておきます。

f:id:ogyahogya:20170202145056p:plain

つまり、 $[X,Y]=0$ なら $X$ と $Y$ の積は可換です。

次の結果が重要です。

f:id:ogyahogya:20170202151228p:plain

これを応用して、以下の結果が得られます。

f:id:ogyahogya:20170202151802p:plain

これは指数関数の値域は一般線形群 ${\rm GL}(n,{\bf R})$ であることを意味しています。

f:id:ogyahogya:20170202152621p:plain

さらに、以下の結果も成り立ちます。

f:id:ogyahogya:20170202152800p:plain

これらより、 $X\in {\bf R}^{n\times n}$ に対して、 $\gamma(t)=\exp(tX)$ は加法群 ${\bf R}$ から ${\rm GL}(n,{\bf R})$ への微分可能な準同型写像 $\gamma:{\bf R}\rightarrow {\rm GL}(n,{\bf R})$ を与えていることが分かります。この曲線 $\gamma$ は実は次のように $\dot{\gamma}(0)$ を用いて表されます。

f:id:ogyahogya:20170202154506p:plain

●行列の対数関数

実数 $x$ の対数関数 $\log x$ を $x=1$ の周りでテイラー展開すると $\log x = \sum_{k=1}^{\infty} \frac{(-1)^{k-1}}{k} (x-1)^k$ でした。これと形式的に同じになるように行列の対数関数が次のように定義されます。

f:id:ogyahogya:20170206140134p:plain

上のように、一般の行列 $A\in {\bf R}^{n\times n}$ に対しては $A$ が単位行列に近いときに対数関数 $\log(A)$ は定義できます。

次の結果は $\exp$ は $0$ の近傍と $I_n$ の近傍の間の微分同相写像であり、逆写像は $\log$ で与えられることを示しています。

f:id:ogyahogya:20170206140629p:plain

この対数関数を利用して、次の公式が得られます。

f:id:ogyahogya:20170206144838p:plain

上の公式は $X$ と $Y$ が可換でないときには指数関数 $\exp X$ と $\exp Y$ の積にカッコ積 $[ X, Y ]$ の影響が出てくることを表現しています。

●参考文献

記事を書くにあたって、以下の本を参考にしました。

別冊数理科学演習形式で学ぶリー群・リー環 2012年 03月号 [雑誌]

出版社/メーカー: サイエンス社
発売日: 2012/03/21
メディア: 雑誌
この商品を含むブログを見る

2017-01-30

等質空間

多様体とか

この記事では、等質空間の概念について説明します。等質空間なるものをなぜ紹介するかというと、また別の記事で実数を成分に持つ正定値対称行列全体の集合 ${\rm Sym}_+(n, {\bf R})$ を幾何学的に考えたいからです。そのような集合を考えたい理由は、 ${\rm Sym}_+(n, {\bf R})$ 上での最適化問題が工学の問題を考えていると自然に出てくるからです。実際の問題の例はまた今度書くと思いますが、この記事では等質空間について説明します。

●群

等質空間の定義を理解するためには、群の概念を知っている必要がありますので、群の定義を確認しておきましょう。

f:id:ogyahogya:20170126125302p:plain

実数や整数は馴染みがあると思いますが、実数全体の集合や整数全体の集合は和に関して群になっています（単位元は両方とも0)。しかし、実数全体の集合は積に関して群になっていません。0の逆元が存在しないからです。同様に、整数全体の集合も積に関しては逆元が存在しないので、積に関して群になっていません。

重要な群の例に次の一般線形群があります。

f:id:ogyahogya:20170126133611p:plain

${\rm GL}(n,{\bf R})$ が通常の行列の積に関して群になっていることは次のように確かめられます。結合法則が成り立つことは、一般線形群の要素が行列であり、行列の積は結合法則を満たすことから言えます。次に、単位元の存在は、単位行列が単位元になることから言えます。最後に、逆元の存在ですが、任意の $A\in {\rm GL}(n,{\bf R})$ に対して $\det A\neq 0$ なので言えます。

$H\subset G$ が部分群であるとは、 $H$ が $G$ の演算によって群になることを言います。一般線形群 ${\rm GL}(n,{\bf R})$ の部分群の重要な例に次の直交群があります。

f:id:ogyahogya:20170126135942p:plain

●群の左剰余類への分解

群の部分群が与えられたら以下のように左剰余類というものを考えることができます。

f:id:ogyahogya:20170130143542p:plain

左剰余類の概念を使って、考えている群の上に以下のように同値関係を導入することができます。

f:id:ogyahogya:20170130143705p:plain

しがたって、同値関係 $\sim$ による商集合を考えることができます。左剰余類を使った同値関係による商集合は次のように表されることが多いです。

f:id:ogyahogya:20170130143931p:plain

商集合という概念はこちらの記事で解説しましたので、興味があったら見てください。

ogyahogya.hatenablog.com

●群の作用

群は集合の要素を変換する役目があります。つまり、 $G$ を群、 $X$ を集合とした時、写像 $f: G\times X \rightarrow X$ が与えられるという形で群は登場することが多いです。この $f(g,x)$ を単に $g\cdot x$ と書くことにします ( $g\in G, x\in X$ )。

f:id:ogyahogya:20170126141331p:plain

群の作用でも特に推移的に作用することが大事です。

f:id:ogyahogya:20170126154633p:plain

定義から、群が集合に推移的に作用していれば、集合の一つの元に群のある要素をかけることによって集合の任意の元が得られることを意味しています。

例えば、一般線形群 ${\rm GL}(n,{\bf R})$ は正定値対称行列全体の集合 ${\rm Sym}_+(n,{\bf R})$ に次のように推移的に作用します。

f:id:ogyahogya:20170126154646p:plain

したがって、 ${\rm Sym}_+(n,{\bf R})$ の任意の元は ${\rm Sym}_+(n,{\bf R})$ の単位元である単位行列に ${\rm GL}(n,{\bf R})$ のある元を作用させること得られます。

●等質空間

この記事で解説したかった等質空間は次のように定義されます。

f:id:ogyahogya:20170130161010p:plain

上で示したことから、正定値対称行列全体の集合 ${\rm Sym}_+(n,{\bf R})$ は等質空間ということになります。

これから集合が等質空間だったら何が言えるかを見ていきましょう。そのために、まず集合の要素を動かさない群の要素の集まりである等方部分群を定義します。

f:id:ogyahogya:20170130144849p:plain

集合 $X$ に作用する群 $G$ の等方部分群 $G_x$ は名前の通り、 $G$ の部分群になっています。よって、等方部分群 $G_x$ によって群 $G$ 上に同値関係を導入できて、その商集合 $G/G_x$ を考えることができます。実は等質空間 $X$ は商集合 $G/G_x$ と次のように同一視できます。

f:id:ogyahogya:20170130145330p:plain

この定理は次のように証明できます。

f:id:ogyahogya:20170130152522p:plain

この定理を使うと、以下のように正定値対称行列全体の集合という等質空間を一般線形群の直交群による商集合として考えられることが分かります。

f:id:ogyahogya:20170130161310p:plain

この事実が正定値対称行列全体の集合のリーマン幾何学を考える際に役立ちます（これについてはそのうち書くと思います。）。

●参考文献

この記事を書く際に以下の本を参考にしました。

代数概論 (数学選書)

作者: 森田康夫
出版社/メーカー: 裳華房
発売日: 1987/11
メディア: 単行本
購入: 1人クリック: 7回
この商品を含むブログ (4件) を見る

2017-01-28

商集合

集合と位相

この記事では、商集合という概念について説明します。この概念を理解しないと、少し高度な数学は理解できないというぐらい重要な概念です。

●同値関係

同値関係という概念を使って商集合は定義されます。同値関係よりも一般的な二項関係の概念は以下の通りです。

f:id:ogyahogya:20170127122158p:plain

$(a,b)\in R$ のとき、 $aRb$ と書きます。

例えば、 $\leq := \{ (a,b)\in {\bf R}\times {\bf R} | a-bは0以下\}$ は二項関係であり、 $(1,2)\in \leq$ なので $1\leq 2$ と書こうというわけです。

$S$ を任意の集合として、 $\mathcal{P}(S)$ を $S$ のベキ集合として、 $\subset := \{ (A,B)\in \mathcal{P}(S)\times \mathcal{P}(S)\,|\, a\in B\,\, \forall a\in A\}$ とすると $\subset$ は二項関係であり、 $\{1,2\}\times \{1,2,3\} \in \subset$ となるので、 $\{1,2\} \subset \{1,2,3\}$ と書こうというわけです。

${\rm People}$ をすべての人間の集合として、 $\Rightarrow := \{ (x,y)\in {\rm People} \times {\rm People}\, |\, x\,\, {\rm loves}\,\, y\}$ と定義すると、 $\Rightarrow$ は二項関係であり、 ${\rm 私} \Rightarrow 妻$ かつ $妻 \Rightarrow 私$ が成り立ちます。

同値関係は以下のように定義されます。

f:id:ogyahogya:20170127123922p:plain

例えば、整数全体の集合 ${\bf Z}$ には以下のような同値関係が考えられます。

f:id:ogyahogya:20170128105230p:plain

上で定義した二項関係 $\leq$ は同値関係になっていません。なぜなら、対称律が成り立たないためです。実際に、 $1\leq 2$ ですが、 $2\leq 1$ とはならないため、対称律は成り立たないことが分かります。また、上で定義した $\subset$ は同値関係ではありません。なぜなら、対称律を満たさないからです。さらに、上で定義した $\Rightarrow$ は同値関係になりません。なぜなら、反射律、対称律、推移律が成り立ちそうにないからです(特に対称律が成り立たないのは残念です)。

●商集合

集合に同値関係を定めることで、その集合を分割できます。対象としている集合の要素で同値なものを集めた集合を同値類と呼びます。

f:id:ogyahogya:20170128110616p:plain

例えば、上で整数全体の集合 ${\bf Z}$ 上に同値関係 $\sim_2$ を定義しましたが、これを使うと以下の同値類が作れます。

f:id:ogyahogya:20170128113102p:plain

同値関係 $\sim_2$ の定義から以下が成り立つことが分かります。

f:id:ogyahogya:20170128113415p:plain

これは同値関係 $\sim_2$ のもとでは、整数全体の集合 ${\bf Z}$ は [0] と [1] によってなる事を意味しています。つまり、以下が成り立ちます。

f:id:ogyahogya:20170128113433p:plain

このように、集合 $S$ に同値関係 $\sim$ が定められると、その集合を同値類によって直和分解できます。

同値類全体の集合を商集合と呼び、以下のように書きます。

f:id:ogyahogya:20170128114155p:plain

例えば、 ${\bf Z}$ の $\sim_2$ による商集合は以下のようになります。

f:id:ogyahogya:20170128114516p:plain

このように商集合は集合の集合になっています。

●同値関係による写像の分解

$S/\sim$ の要素である $a\in S$ の同値類を $\bar{a}$ と書くことにすると、以下の $S$ の $S/\sim$ への自然な写像と呼ばれる写像を定義できます。

f:id:ogyahogya:20170128120008p:plain

二つの集合間の写像が与えられると、その写像を使って同値関係を以下のように定義できます。

f:id:ogyahogya:20170128120942p:plain

この同値関係を使うことで、写像が以下のように分解できます。

f:id:ogyahogya:20170128132959p:plain

とくに、写像 $f$ が全射であるなら以下の可換図式が得られます。

f:id:ogyahogya:20170128133140p:plain

●参考文献

記事を書くにあたって、以下の本を参考にしました。

集合・位相入門

作者: 松坂和夫
出版社/メーカー: 岩波書店
発売日: 1968/06/10
メディア: 単行本
購入: 12人クリック: 62回
この商品を含むブログ (56件) を見る

2016-05-19

凸解析

最適化

この記事では最適化理論の基盤となる凸解析の理論を解説します。

●最適化問題とは

目的関数と呼ばれる関数 $f:{\bf R}^n\rightarrow {\bf R}$ を制約条件 $x\in S \subset {\bf R}^n$ のもとで最小化する問題を最適化問題と呼びます。特に、 $f$ が凸関数で、 $S$ が凸集合である時、凸最適化問題と呼びます。凸最適化問題は効率的に解く方法がたくさん研究されています。

●凸集合と凸関数と凹関数

次の性質を満たす集合を凸集合と呼びます。

f:id:ogyahogya:20160517164152p:plain

つまり、ある集合の任意の２点を結んだ線分がその集合に含まれるなら、その集合は凸集合です。凸集合と非凸集合のイメージ図は次のような感じになります。

f:id:ogyahogya:20160517164353p:plain

次の性質を満たす関数を凸関数と呼びます。

f:id:ogyahogya:20160517164505p:plain

凸関数と非凸関数のイメージ図は次のような感じになります。

f:id:ogyahogya:20160517173323p:plain

凸集合と凸関数はエピグラフという概念を通じて関係付けることができます。

f:id:ogyahogya:20160517173418p:plain

例えば、次のようにエピグラフを図示することができます。

f:id:ogyahogya:20160517173512p:plain

凸集合と凸関数は次の関係があります。

f:id:ogyahogya:20160517173611p:plain

凸関数は最小化のしやすい関数ですが、最大化のしやすい関数としては次の凹関数があります。

f:id:ogyahogya:20160518161105p:plain

●狭義凸関数

凸関数は最小化しやすい関数ですが、最小値を与える点は一つとは限りません。最小値を与える点が存在すれば一つである凸関数を狭義凸関数と言います。

f:id:ogyahogya:20160519093017p:plain

f:id:ogyahogya:20160519093049p:plain

f:id:ogyahogya:20160519093101p:plain

狭義凸関数だからといって、最小値が必ず存在するとは限りません。最小値の存在しない狭義凸関数の例としては $x$ や $e^x$ があります。

●凸集合と凸関数の性質（極一部）

任意の数の凸集合の共通部分は凸集合になります。

f:id:ogyahogya:20160518163118p:plain

ある集合上の点によってパラメトライズされた凸関数は、そのパラメータについての上限を取っても凸関数となります。つまり、以下が成り立ちます。

f:id:ogyahogya:20160518163936p:plain これにより、凸関数の共役関数が凸関数になることが保障されます(共役関数は今度紹介します)。また、これが

で紹介したレート関数が凸関数になる理由です。これが成り立つことは次の関係式より分かります。

f:id:ogyahogya:20160518171916p:plain

実際に、 $f(x,y)$ は $x$ について凸関数なので、 ${\rm epi}\, f(\cdot,y)$ は凸集合となり、凸集合の共通部分は凸集合であることから ${\rm epi}\, g$ も凸集合となる事が分かり、その結果 $g$ は凸関数となることが分かります。上の関係式は以下のように証明できます。

f:id:ogyahogya:20160518172255p:plain

凹関数に関しても次のように同様の関係が成り立ちます。

f:id:ogyahogya:20160518172353p:plain これにより、ラグランジアンから双対関数を定義したときに、双対関数が凹関数になることが保障されます(ラグランジアンと双対関数は今度紹介します)。

●微分可能な凸関数

微分可能な凸関数は次のように特徴付けられます。

f:id:ogyahogya:20160519094417p:plain

これは

f:id:ogyahogya:20160519094446p:plain

を意味していて、

f:id:ogyahogya:20160519094509p:plain

というような関係にあるということです。

また、微分可能な凸関数の最小値を与える点は勾配がゼロになる点です。

f:id:ogyahogya:20160519094910p:plain

●勾配情報の重要性

微分可能な関数 $f(x)$ は勾配 $\nabla f(x)$ を求めることができます。勾配の情報は関数の最小化を考えるにあたって便利です。このことを実感するために、次のようなユークリッド空間上の制約なしの最小化問題を考えましょう。

f:id:ogyahogya:20160519110919p:plain

ただし、目的関数 $f$ は微分可能な凸関数であるとします。この問題を解くためには、現在の点を $x_k$ としたときに $f$ が減少する方向に進んでいけば良いです。つまり、

f:id:ogyahogya:20160519111247p:plain

の $\eta_k$ が $f$ の減少する方向であれば良いわけです。目的関数 $f$ が減少する方向を調べるには点 $x_k$ から微小に動いたときの $f$ の関数値がどのように変化するかを調べれば良いわけで、そのようなことを調べるためには

f:id:ogyahogya:20160519112446p:plain

を $t=0$ で微分すれば良いです ( $g_{\eta_k}$ の $t=0$ での微分は $f$ の点 $x_k$ での $\eta_k$ 方向の微分を意味しているので)。そこで、関数 $g_{\eta_k}$ の $t=0$ での微分を計算してみると

f:id:ogyahogya:20160519112808p:plain

となります。よって、現在の点 $x_k$ から $\nabla f(x_k)$ の逆方向に進むと目的関数 $f$ は減少するということが分かります。このことをもとに、進行方向を表す $\eta_k$ を

f:id:ogyahogya:20160519122030p:plain

とした最適化アルゴリズムを最急降下法と呼びます。目的関数 $f$ が微分可能な凸関数であれば $\nabla f(x_k)=0$ が点 $x_k$ で最小値を取っている証となるので最急降下法のようなアルゴリズムを $\nabla f(x_k)\approx 0$ となるまで単純に反復すれば良いということになります。このように勾配情報は凸関数の最小化を実行するにあたって重要な情報となります。

●劣微分と劣勾配

上で勾配情報は凸関数の最小化を実行するにあたって重要だと述べましたが、凸関数は必ずしも微分可能であるとは限りません。例えば、 $|x|$ は凸関数ですが、 $x=0$ で微分可能ではありません。しかし、勾配のようなものを微分可能でない凸関数に対しても定義することができます。まず、微分可能な凸関数 $f$ の点 $x$ での勾配 $\nabla f(x)$ はエピグラフ ${\rm epi}\, f$ の点 $x$ における支持超平面を特徴付けたことを思い出しましょう。この支持超平面は $\alpha= f(x)+\nabla f(x)^T (y-x)$ を満たす点 $(y,\alpha)$ から形成されていました。微分可能でない凸関数 $f$ に対しても、エピグラフ ${\rm epi}\, f$ の点 $x$ における支持超平面を考えることができ、その支持超平面を特徴付ける「勾配のようなもの」の集まりを劣微分と言います。