この記事では最適化理論の基盤となる凸解析の理論を解説します。
●最適化問題とは
目的関数と呼ばれる関数 を制約条件
のもとで最小化する問題を最適化問題と呼びます。特に、
が凸関数で、
が凸集合である時、凸最適化問題と呼びます。凸最適化問題は効率的に解く方法がたくさん研究されています。
●凸集合と凸関数と凹関数
次の性質を満たす集合を凸集合と呼びます。

つまり、ある集合の任意の2点を結んだ線分がその集合に含まれるなら、その集合は凸集合です。凸集合と非凸集合のイメージ図は次のような感じになります。

次の性質を満たす関数を凸関数と呼びます。

凸関数と非凸関数のイメージ図は次のような感じになります。

凸集合と凸関数はエピグラフという概念を通じて関係付けることができます。

例えば、次のようにエピグラフを図示することができます。

凸集合と凸関数は次の関係があります。

凸関数は最小化のしやすい関数ですが、最大化のしやすい関数としては次の凹関数があります。

●狭義凸関数
凸関数は最小化しやすい関数ですが、最小値を与える点は一つとは限りません。最小値を与える点が存在すれば一つである凸関数を狭義凸関数と言います。



狭義凸関数だからといって、最小値が必ず存在するとは限りません。最小値の存在しない狭義凸関数の例としては や
があります。
●凸集合と凸関数の性質(極一部)
任意の数の凸集合の共通部分は凸集合になります。

ある集合上の点によってパラメトライズされた凸関数は、そのパラメータについての上限を取っても凸関数となります。つまり、以下が成り立ちます。
 これにより、凸関数の共役関数が凸関数になることが保障されます(共役関数は今度紹介します)。また、これが
これにより、凸関数の共役関数が凸関数になることが保障されます(共役関数は今度紹介します)。また、これが
で紹介したレート関数が凸関数になる理由です。これが成り立つことは次の関係式より分かります。

実際に、 は
について凸関数なので、
は凸集合となり、凸集合の共通部分は凸集合であることから
も凸集合となる事が分かり、その結果
は凸関数となることが分かります。上の関係式は以下のように証明できます。

凹関数に関しても次のように同様の関係が成り立ちます。
 これにより、ラグランジアンから双対関数を定義したときに、双対関数が凹関数になることが保障されます(ラグランジアンと双対関数は今度紹介します)。
これにより、ラグランジアンから双対関数を定義したときに、双対関数が凹関数になることが保障されます(ラグランジアンと双対関数は今度紹介します)。
●微分可能な凸関数
微分可能な凸関数は次のように特徴付けられます。

これは

を意味していて、

というような関係にあるということです。
また、微分可能な凸関数の最小値を与える点は勾配がゼロになる点です。

●勾配情報の重要性
微分可能な関数 は勾配
を求めることができます。勾配の情報は関数の最小化を考えるにあたって便利です。このことを実感するために、次のようなユークリッド空間上の制約なしの最小化問題を考えましょう。

ただし、目的関数 は微分可能な凸関数であるとします。この問題を解くためには、現在の点を
としたときに
が減少する方向に進んでいけば良いです。つまり、

の が
の減少する方向であれば良いわけです。目的関数
が減少する方向を調べるには点
から微小に動いたときの
の関数値がどのように変化するかを調べれば良いわけで、そのようなことを調べるためには

を で微分すれば良いです (
の
での微分は
の点
での
方向の微分を意味しているので)。 そこで、関数
の
での微分を計算してみると

となります。よって、現在の点 から
の逆方向に進むと目的関数
は減少するということが分かります。このことをもとに、進行方向を表す
を

とした最適化アルゴリズムを最急降下法と呼びます。目的関数 が微分可能な凸関数であれば
が点
で最小値を取っている証となるので最急降下法のようなアルゴリズムを
となるまで単純に反復すれば良いということになります。このように勾配情報は凸関数の最小化を実行するにあたって重要な情報となります。
●劣微分と劣勾配
上で勾配情報は凸関数の最小化を実行するにあたって重要だと述べましたが、凸関数は必ずしも微分可能であるとは限りません。例えば、 は凸関数ですが、
で微分可能ではありません。しかし、勾配のようなものを微分可能でない凸関数に対しても定義することができます。まず、微分可能な凸関数
の点
での勾配
はエピグラフ
の点
における支持超平面を特徴付けたことを思い出しましょう。この支持超平面は
を満たす点
から形成されていました。微分可能でない凸関数
に対しても、エピグラフ
の点
における支持超平面を考えることができ、その支持超平面を特徴付ける「勾配のようなもの」の集まりを劣微分と言います。

そして、劣微分の要素である「勾配のようなもの」を劣勾配と言います。

劣勾配は通常の勾配の一般化になっていることが次の性質が成り立つことから分かります。

つまり、凸関数が微分可能だったら劣勾配は勾配と一致するというわけです。また、ある点における劣微分がゼロを含んでいたら(劣勾配にゼロのものがあったら)、その点で関数は最小値をとります。

劣微分の計算方法を具体例で示しておきます。

上の という微分可能でない凸関数は、スパースな解が期待できるような最適化問題(最適解の成分はたくさんゼロになると期待できるような問題)によく利用されています。
●参考文献
(1) もっと数学的に細かいことが書いています。
(2) スパースな解が期待できるような最適化問題について解説しています。

スパース性に基づく機械学習 (機械学習プロフェッショナルシリーズ)
- 作者: 冨岡亮太
- 出版社/メーカー: 講談社
- 発売日: 2015/12/19
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る





























































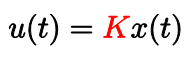
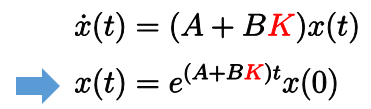

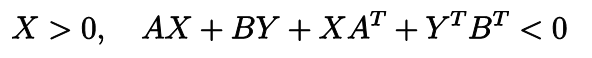
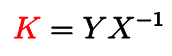






 例えば、
例えば、



















































