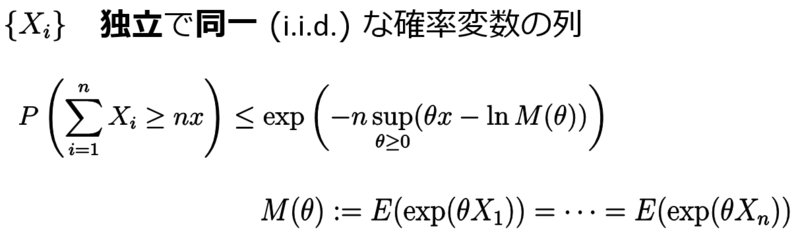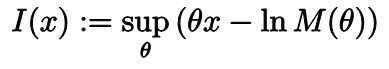制御の目的は対象とするシステムに適切な入力を加えて所望の出力を実現することです。

この記事では制御を実行する手順と、システムの最も重要な数学モデルである線形システムについて説明します。
●制御の手順
制御するときに考える入力や出力は一つだけとは限らず、複数ある場合が多いです。例えば、車の運転は次の図のように入力数3で出力数2だと考えられます。

制御を行う手順は次のようになります。

まず、モデリングは対象とするシステムの数学モデルを立てることを意味しています。数学モデルは物理法則や実験から得られたデータで作られます。次に制御器の設計は対象とするシステムを制御するための入力を設計することを意味しています。これはモデリングによって得られた数学モデルを使って行われます。数学モデルが非常に複雑だと制御器を作れないことがあり、その場合はモデリングをやり直します。制御器が設計できたら、シミュレーションをしてその制御器で対象とするシステムがきちんと制御できてるか確認します。これがダメなら制御器の設計やモデリングをやり直します。シミュレーションで上手くいったら制御器を実装します。シミュレーションの段階では、すべて数学モデルを使っているため上手くいったが、現実の対象システムと数学モデルのギャップが大きすぎて上手くいかないことがあります。その場合には対象システムと数学モデルのギャップを縮めるためにモデリングからやり直します。制御器を実装して目標通り動いたら完成です。
車の運転の例では人は脳内に車のモデルを立ててると考えることができます(数学モデルではないと思いますが)。制御器は人の脳で、何度も運転をすることによって立派な制御器が得られます。運転免許証は車を運転するための制御器が脳内にできた証だと考えられます。
●モデリングの例
制御のための入力を設計するためには数学モデルがあったら便利です。モデリングは物理法則や入出力データを利用します。例えば、次のマス・バネ・ダンパー系を考えましょう。

上のマス・バネ・ダンパー系はニュートンの運動方程式を表していて2階の微分方程式となっています。
制御工学では1階の微分方程式で表されるシステムを対象システムとすることが多く、1階の微分方程式でシステムを表現できたら制御工学の多くの成果が利用できます。上のマス・バネ・ダンパー系を1階の微分方程式へ変換することは容易です。実際に次のように変換できます。

という新しい変数が出てきていますが、これを状態と呼びます。上の微分方程式系は状態方程式と言われているものです。次にこれを説明します。
●システムの状態方程式表現
システムの数学的な表現の一つに状態方程式表現と言われているものがあります。これは1960年頃にKalmanによって導入された表現で、現在では制御理論の研究分野で最もよく利用されている表現となっています。システムの状態方程式表現は次のような方程式系のことです。

システムが上の状態方程式で表されるとき、そのシステムは線形システムであると言います。線形というのは変数について線形だからです。
線形システムは非常に重要です。なぜなら多くのシステムが線形システムで近似できるからです。例えば、次のような非線形システムは平衡点まわりでは線形システムで近似できます。

また、偏微分方程式系も線形システムとして近似できます。例えば、次のようにできます。



●線形システムの制御
線形システムを制御することを考えます。ここでは簡単のために の場合を考えます。まず、状態方程式の解を調べてどのような制御が必要になるか考えてみましょう。状態方程式の解は次のようになります。

ここで、次のように何も入力を加えないとすると解は

となります。よって、

となることが分かります。つまり、入力を加えなかったら状態が発散する恐れがあります。これを防ぐために

という設計問題を考えるのは自然です。ただし、は目標状態とします。これは次のようなフィードバックを利用することで実現されることがあります。

次のように定数行列として与えられた制御器が最も簡単なものです。

これは入力を

としたことに相当します。このとき

となります。よって

となります。このような は線形行列不等式(LMI)

の解 を用いて

と与えることができることが知られています。
上のようなLMI制約を満たす変数の集合は凸集合となります。制御工学の分野では上のようなLMI制約のもとで、ある凸関数で表された評価関数を最小化(最大化)して制御器を設計せよという研究が盛んに行われていた時期がありました(今でも結構あります)。この問題は凸最適化問題となるため、最適化理論の分野でよく研究された成果を利用することができます。しかし、線形システム以外のシステムに対しては制御器の設計問題を凸最適化問題へ帰着させることは困難です。つまり、対象システムを線形システムとしてモデリングしなかったら制御器の設計は非常に難しくなります。対象システムを線形システムとしてモデリングすることは制御器の設計を簡単に行う上でも重要です。

●参考文献
(1) タイトルの通り制御工学の考え方が分かりやすく書いています。

制御工学の考え方―産業革命は「制御」からはじまった (ブルーバックス)
- 作者: 木村英紀
- 出版社/メーカー: 講談社
- 発売日: 2002/12/16
- メディア: 新書
- 購入: 3人 クリック: 12回
- この商品を含むブログ (11件) を見る
(2) 線形システムの制御器の設計が凸最適化問題に帰着することが分かりやすく書いています。

LMIによるシステム制御 - ロバスト制御系設計のための体系的アプローチ
- 作者: 蛯原義雄
- 出版社/メーカー: 森北出版
- 発売日: 2012/03/08
- メディア: 単行本(ソフトカバー)
- クリック: 1回
- この商品を含むブログを見る




 例えば、
例えば、